
【题目】两个反比例函数y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
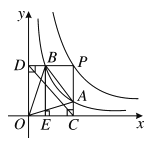
的图象于点B,BE⊥x轴于点E,当点P在y=![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)

【答案】①③④
【解析】试题解析:作![]() 轴于
轴于![]()
正确.∵A、B在![]() 上,
上,
![]()
![]()
∴OCAC=OEBE,
∵OC=PD,BE=PC,
∴PDAC=DBPC,
![]()
∴![]() .故此选项正确。
.故此选项正确。
②错误,不一定,只有当四边形OCPD为正方形时满足PA=PB;
③正确,由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化;故此选项正确。
④正确.∵△ODB的面积=△OCA的面积![]()
∴△ODB与△OCA的面积相等,同理可得:![]()
∵S△OBA=S矩形OCPDS△ODBS△BAPS△AOC,
S四边形ACEB= S矩形OCPDS△ODBS△BAPS△OBE
∴S△OBA = S四边形ACEB,故此选项正确,
故一定正确的是①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,![]() 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:

(1)画线段![]() ,且使
,且使![]() ,连接
,连接![]() ;
;
(2)线段![]() 的长为________,
的长为________,![]() 的长为________,
的长为________,![]() 的长为________;
的长为________;
(3)![]() 是________三角形,四边形
是________三角形,四边形![]() 的面积是________;
的面积是________;
(4)若点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() ,则
,则![]() 的度数为________.
的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,已知该小区用水量不超过![]() 的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
级别 |
|
|
|
|
|
|
月均用水量 |
|
|
|
|
|
|
频数(户) | 6 | 12 |
| 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)补全频率分布直方图;

(3)若将调查数据绘制成扇形统计图,则月均用水量“![]() ”的圆心角度数是 .
”的圆心角度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,动点
,动点![]() 同时从
同时从![]() 两点出 发,分别沿
两点出 发,分别沿![]() 方向匀速移动,动点
方向匀速移动,动点![]() 的速度是
的速度是![]() ,动点
,动点![]() 的速度是
的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 两点停止运动,连接
两点停止运动,连接![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() ,试解答下面的问题:
,试解答下面的问题:
![]() 当
当![]() 时,求
时,求![]() 的面积?
的面积?
![]() 当
当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的角平分线上,若存在,请求出
的角平分线上,若存在,请求出![]() 的值;若不存 在,请说明理由?
的值;若不存 在,请说明理由?
![]() 请用含有
请用含有![]() 的代数式表示四边形
的代数式表示四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB=2![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
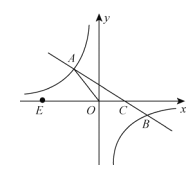
【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 在
在![]() 上,且
上,且![]() ,设
,设![]() .
.

(1)当![]() 时,如图2,求
时,如图2,求![]() 的长;
的长;

(2)设![]() ,求
,求![]() 关于
关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com