
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )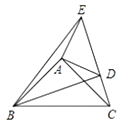
A.4
B.3
C.2
D.1
【答案】B
【解析】①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
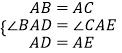 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,本选项正确;②∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,本选项正确;③∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵∠ABD=∠ACE
∴∠ACE+∠DBC=45°,本选项正确;④∵∠ABD=∠ACE,
∴只有当∠ABD=∠DBC时,∠ACE=∠DBC才成立。
综上所述,正确的结论有3个.
所以答案是:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位长度得到点
个单位长度得到点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交反比例函数
轴的平行线交反比例函数![]() 的图象于点
的图象于点![]() ,
,![]() .
.
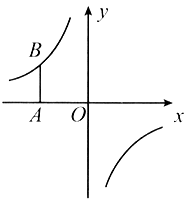
(1)求反比例函数的解析式;
(2)若![]() 、
、![]() 是该反比例函数图象上的两点,且
是该反比例函数图象上的两点,且![]() 时,
时,![]() ,指出点
,指出点![]() 、
、![]() 各位于哪个象限?并简要说明理由.
各位于哪个象限?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]() 上.
上.
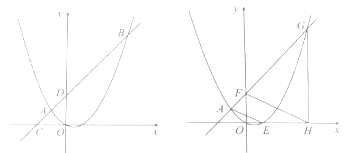
(1)求抛物线的解析式;
(2)如图1,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,设抛物线与
,设抛物线与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() ,求证
,求证![]() ;
;
(3)如图2,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() 两点,点
两点,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向匀速运动,速度为每秒
方向匀速运动,速度为每秒![]() 个单位长度,同时点
个单位长度,同时点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向匀速运动,速度为每秒1个单位长度,点
轴正方向匀速运动,速度为每秒1个单位长度,点![]() 是直线
是直线![]() 与抛物线的一个交点,当运动到
与抛物线的一个交点,当运动到![]() 秒时,
秒时,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将9.52变形正确的是( )
A. 9.52=92+0.52 B. 9.52=(10+0.5)(10﹣0.5)
C. 9.52=102﹣2×10×0.5+0.52 D. 9.52=92+9×0.5+0.52
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com