
【题目】 已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根
有两个实数根![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
【答案】(1)m≤5;(2)4.
【解析】
试题分析:(1)根据方程的系数结合根的判别式,即可得出△=20﹣4m≥0,解之即可得出结论;
(2)由根与系数的关系可得x1+x2=6①、x1x2=m+4②,分x2≥0和x2<0可找出3x1=x2+2③或3x1=﹣x2+2④,联立①③或①④求出x1、x2的值,进而可求出m的值.
试题解析:(1)∵关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,
∴△=(﹣6)2﹣4(m+4)=20﹣4m≥0,
解得:m≤5,
∴m的取值范围为m≤5.
(2)∵关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,
∴x1+x2=6①,x1x2=m+4②.
∵3x1=|x2|+2,
当x2≥0时,有3x1=x2+2③,
联立①③解得:x1=2,x2=4,
∴8=m+4,m=4;
当x2<0时,有3x1=﹣x2+2④,
联立①④解得:x1=﹣2,x2=8(不合题意,舍去).
∴符合条件的m的值为4.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )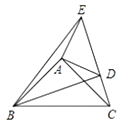
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
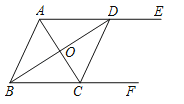
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() .
.
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹:
①以点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交边
的长为半径画弧交边![]() 于点
于点![]() ,连接
,连接![]() ;
;
②作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;
;
③连接![]() ;
;
(2)在(1)作出的图形中,若![]() ,则
,则![]() 的值为 .
的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式m2(a﹣2)+m(2﹣a)分解因式等于( )
A.(a﹣2)(m2+m)
B.(a﹣2)(m2﹣m)
C.m(a﹣2)(m﹣1)
D.m(a﹣2)(m+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.和为180°的两个角是邻补角B.内错角相等
C.经过直线外一点有且只有一条直线与这条直线平行D.同旁内角相等,两直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com