
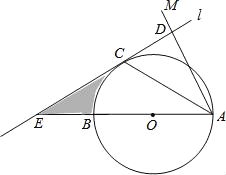
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°.求图中所示阴影部分的面积.
【答案】(1)CD与⊙O相切.理由见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OC,如图,由∠1=∠2,∠2=∠3得∠1=∠3,则可判断OC∥AD,由于CD⊥AD,所以OC⊥CD,于是根据切线的判定定理可得CD为⊙O的切线;
(2)利用三角形外角性质可得到∠EOC=60°,而OC⊥CD,则∠OCE=90°,在Rt△OCE中利用∠EOC的正切可计算出CE=3![]() ,然后三角形面积公式和扇形面积公式,利用S阴影部分=S△OOE-S扇形COB进行计算即可.
,然后三角形面积公式和扇形面积公式,利用S阴影部分=S△OOE-S扇形COB进行计算即可.
试题解析:(1)CD与⊙O相切.理由如下:
连结OC,如图,
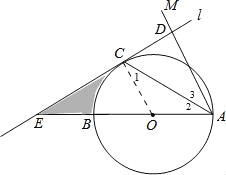
∵OA=OC,
∴∠1=∠2,
∵∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
而CD⊥AD,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵∠EOC=∠1+∠2,∠2=30°,
∴∠EOC=60°,
∵OC⊥CD,
∴∠OCE=90°,
在Rt△OCE中,∵tan∠EOC=![]() ,
,
∴CE=3tan60°=3![]() ,
,
∴S阴影部分=S△OOE-S扇形COB
=![]()
=![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】几何模型:
条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连结A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
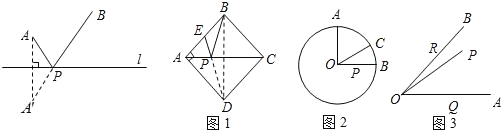
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则PB+PE的最小值是 ;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面现象能说明“面动成体”的是( )
A. 旋转一扇门,门运动的痕迹
B. 扔一块小石子,小石子在空中飞行的路线
C. 天空划过一道流星
D. 时钟秒针旋转时扫过的痕迹
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据甘肃省财政快报统计,2014年全省财政收入672220000000元,67220000000用科学记数法表示为( )
A. 6.722×109 B. 6.722×1010 C. 67.22×109 D. 67.22×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
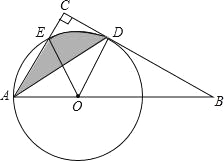
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
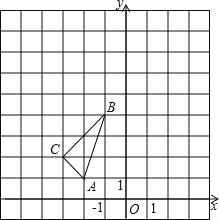
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com