
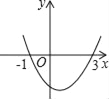
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
【答案】D
【解析】分析:首先根据二次函数图象开口方向可得a>0,根据图象与y轴交点可得c<0,再根据二次函数的对称轴x=-![]() ,结合图象与x轴的交点可得对称轴为x=1,结合对称轴公式可判断出①的正误;根据对称轴公式结合a的取值可判定出b<0,根据a、b、c的正负即可判断出②的正误;利用抛物线与x轴有两个交点即可判断出③的正误;利用当x=4时,y>0,则16a+4b+c>0,由①知,b=-2a,得出8a+c>0,即可判断出④的正误.
,结合图象与x轴的交点可得对称轴为x=1,结合对称轴公式可判断出①的正误;根据对称轴公式结合a的取值可判定出b<0,根据a、b、c的正负即可判断出②的正误;利用抛物线与x轴有两个交点即可判断出③的正误;利用当x=4时,y>0,则16a+4b+c>0,由①知,b=-2a,得出8a+c>0,即可判断出④的正误.
详解:根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,
对称轴:x=![]() >0,
>0,
①∵它与x轴的两个交点分别为(1,0),(3,0),
∴对称轴是x=1,
∴![]() =1,
=1,
∴b+2a=0,
故①正确;
②∵a>0,![]() =1,
=1,
∴b<0,
又∵c<0,
∴abc>0,
故②错误;
③∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,
由①知,b=2a,
∴8a+c>0;
故④正确;
综上所述,正确的结论是:①③④,
故选D.


科目:初中数学 来源: 题型:
【题目】点A,B在数轴上分别表示有理数a,b.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示﹣2和8两点之间的距离是________.
(2)数轴上表示x和﹣4两点A和B之间的距离表示为__________;如果AB=2,那么x=___________.
(3)若点C表示的数为x,当点C在什么位置时,|![]() x+1|+|
x+1|+|![]() x1|取得的值最小,并直接写出最小值。
x1|取得的值最小,并直接写出最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足![]() .
.
(1)写出a、b及AB的距离:a=________;b=________;AB=________.
(2)若动点P从点A出发,以每秒3个点位长度沿数轴向右匀速运动,动点Q从点B出发,以每秒5个单位长度向右匀速运动,若P、Q同时出发,问点Q运动多少秒追上点P?
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
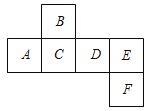
(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,M,N,P,R分别是数轴上的四个整数所对应的点,其中有一个点是原点,并且,MN=NP=PR=1,数a对应的点在M和N之间,数b对应的点在P和R之间,若|a|+|b|=2,则原点是(填M,N,P,R中的一个或几个)_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,点D是边AB的中点,CE∥AB,且AB=2CE,连结BE、CD。

(1)求证:四边形BECD是平行四边形;
(2)用无刻度的直尺画出△ABC边BC上的中线AG(保留画图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别 | 投进个数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
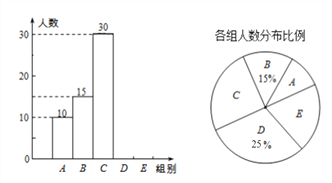
根据以上信息完成下列问题。
①本次抽取的学生人数为多少?
②统计表中的m=__________;
③扇形统计图中E组所占的百分比;
④补全频数分布直方图;
⑤扇形统计图中“C组”所对应的圆心角的度数;
⑥本次比赛中投篮个数的中位数落在哪一组;
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).

(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简![]() ÷(
÷(![]() -
-![]() ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
【答案】4.
【解析】试题分析:先将原分式进行化解,化解过程中注意不为0的量,根据不为0的量结合x的取值范围得出合适的x的值,将其代入化简后的代数式中即可得出结论.
试题解析:原式= =
= =
=![]() .
.
其中 ,即x≠﹣1、0、1.
,即x≠﹣1、0、1.
又∵﹣2<x≤2且x为整数,∴x=2.
将x=2代入![]() 中得:
中得: ![]() =
=![]() =4.
=4.
考点:分式的化简求值.
【题型】解答题
【结束】
21
【题目】解方程:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com