
 在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.
在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.分析 (1)根据题意直接画出图形得出即可;
(2)①利用对称的性质以及等角对等边进而得出答案;
②由轴对称的性质可得:∠PAB=∠PAE=α,AE=AB=AD,分两种情况分别用等腰三角形的性质和平角以及周角的意义计算即可.
解答 解:(1)如图1所示:
(2)①由对称得∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADE=$\frac{180°-130°}{2}$=25°;
②Ⅰ、当0°<α<45°时,如图1,由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=∠BAD+∠BAE=∠BAD+2∠BAP=90°+2α,
∵AE=AB,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$[180°-(90°+2α)]=45°-α;
Ⅱ、当45°<α<90°时,如图2,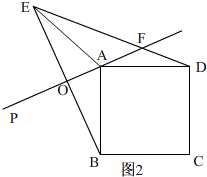
由对称得∠PAB=∠PAE=α,AE=AB=AD,
∴∠BAE=2∠PAB=2α
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=360°-∠BAD-2∠BAP=360°-90°-2α=270°-2α,
∵AE=AB,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$[180°-(270°-2α)]=α-45°.
∴当0°<α<45°时,∠ADE=45°-α,当45°<α<90°时,∠ADE=α-45°.
点评 此题主要考查了正方形的性质以及平角,周角的意义和等腰三角形的性质等知识,利用轴对称的性质得出对应边相等是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 男、女生做代表的可能性一样大 | |
| B. | 男生做代表的可能性大 | |
| C. | 女生做代表的可能性大 | |
| D. | 男、女生做代表的可能性大小不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
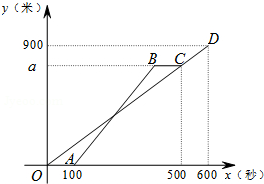 甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=0.7×80(x-20)+80×20 | B. | y=0.7x+80(x-10) | ||
| C. | y=0.7×80•x | D. | y=0.7×80(x-10) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=5x-3 | B. | y=-x-3 | C. | $y=\frac{3x-2}{2}$ | D. | y=5x+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com