
【题目】解不等式组 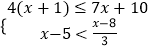 ,并写出它的所有非负整数解.
,并写出它的所有非负整数解.
【答案】解: 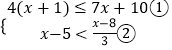 ,
,
由①得:x≥﹣2;
由②得:x< ![]() ,
,
∴不等式组的解集为﹣2≤x< ![]() ,
,
则不等式组的所有非负整数解为:0,1,2,3
【解析】先求出不等式组中每个不等式的解集,再求出其公共解集,即可确定出所有的非负整数解。
【考点精析】解答此题的关键在于理解一元一次不等式组的解法的相关知识,掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ),以及对一元一次不等式组的整数解的理解,了解使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】我们通常用作差法比较代数式大小.例如:已知M=2x+3,N=2x+1,比较M和N的大小.先求M﹣N,若M﹣N>0,则M>N;若M﹣N<0,则M<N;若M﹣N=0,则M=N,反之亦成立.本题中因为MN=2x+3(2x+1)=2>0,所以M>N.
(1)如图1是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S2.用含a的代数式表示S1= ,S2= (需要化简).然后请用作差法比较S1与S2大小;
(2)已知A=2a2﹣6a+1,B=a2﹣4a﹣1,请你用作差法比较A与B大小.
(3)若M=(a﹣4)2,N=16﹣(a﹣6)2,且M=N,求(a﹣4)(a﹣6)的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点 P 以每秒 2cm 的速度沿图甲的边框按从 B→C→D→E→F→A 的路径移动,相应的△ABP 的面积 S 与时间 t 之间 的关系如图乙中的图象表示.若 AB=6cm,则 b=_______.
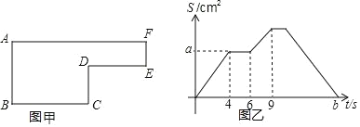
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
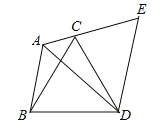
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.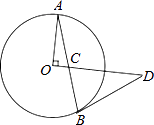
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题共10分)水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
(3)现需按毛利润的10%交纳各种税费,人工费每日按销售量每千克支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每千克涨价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校区内有甲、乙两块大小一样的长方形地块,地块长30m,宽25m,现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分),余下的部分绿化.现已知ABCD1m,EFGH1m,记甲、乙地块的绿化面积分别为S1、S2,则S1、S2的大小关系是( )

A.S1<S2B.S1=S2C.S1>S2D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com