
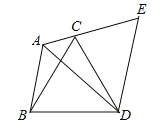
【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
【答案】8
【解析】
只要证明△ADE是等边三角形,即可推出∠EAD=60°,AD=AE,推出∠BAD=∠BAC-∠CAD=60°,推出AD=AE=AC+CE=AC+AB=3+5=8.
∵△ECD 由△ABD 绕点 D 顺时针旋转 60°而得:
∴AD=DE,∠BDA=∠CDE,
∴∠BDC=∠ADE=60°,∠ABD=∠ECD,
∵∠BAC=120°,∠BDC=60°,
∴∠BAC+∠BDC=180°,
∴∠ABD+∠ACD=180°,
∴∠ACD+∠ECD=180°,
∴A、C、E 共线,
∴△ADE 是等边三角形,
∴∠EAD=60°,AD=AE,
∴AD=AE=AC+CE=AC+AB=3+5=8.


科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.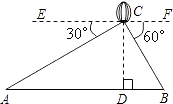
查看答案和解析>>
科目:初中数学 来源: 题型:
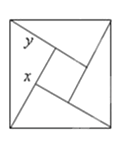
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm
B.7cm
C.12cm
D.17cm或7cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com