
【题目】如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.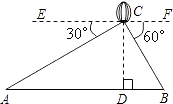
【答案】解:由已知,得∠ECA=30°,∠FCB=60°,CD=90,
EF∥AB,CD⊥AB于点D.
∴∠A=∠ECA=30°,∠B=∠FCB=60°.
在Rt△ACD中,∠CDA=90°,tanA= ![]() ,
,
∴AD= ![]() =90×
=90× ![]() =90
=90 ![]() .
.
在Rt△BCD中,∠CDB=90°,tanB= ![]() ,
,
∴DB= ![]() =30
=30 ![]() .
.
∴AB=AD+BD=90 ![]() +30
+30 ![]() =120
=120 ![]() .
.
答:建筑物A、B间的距离为120 ![]() 米
米
【解析】添加辅助线,将相关的问题转化到直角三角形中求解。过点C作CD⊥AB于点D,根据已知易求得∠A、∠B的度数,再在Rt△ACD和Rt△BCD中,分别求出DB、AD的长,就可以求出AB的长。
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法),以及对关于仰角俯角问题的理解,了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】定义:P、Q分别是两条线段a,b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知,O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
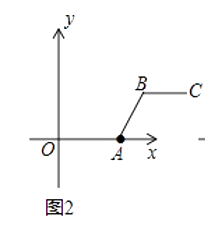
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离为;当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为;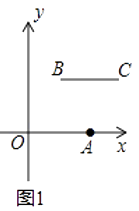
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.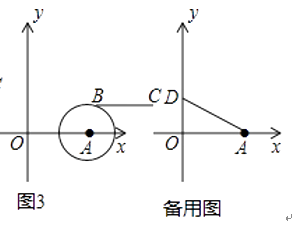
(3)当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点 P 以每秒 2cm 的速度沿图甲的边框按从 B→C→D→E→F→A 的路径移动,相应的△ABP 的面积 S 与时间 t 之间 的关系如图乙中的图象表示.若 AB=6cm,则 b=_______.
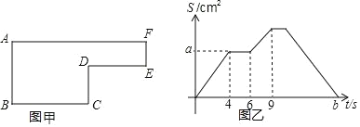
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米.
(2)小明在书店停留了 分钟.
(3)本次上学途中,小明一共行驶了 米.一共用了 分钟.
(4)我们认为骑单车的速度超过 300 米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
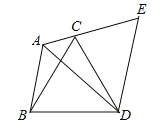
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;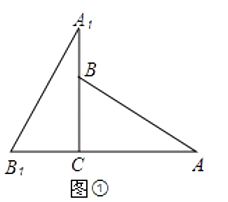
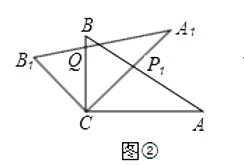
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.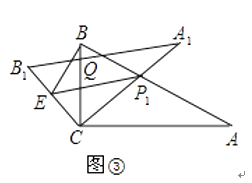
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com