
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;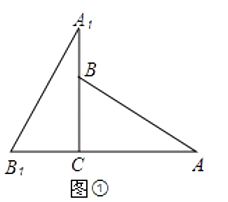
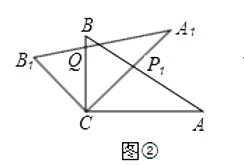
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.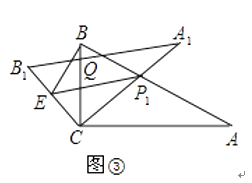
【答案】
(1)证明:∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°,
∵在△B1CQ和△BCP1中,
 ,
,
∴△B1CQ≌△BCP1(ASA),
∴CQ=CP1
(2)解:作P1D⊥CA于D,
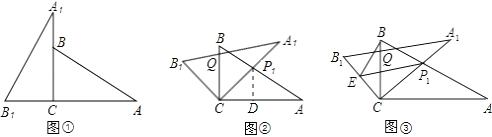
∵∠A=30°,
∴P1D= ![]() AP1=1,
AP1=1,
∵∠P1CD=45°,
∴ ![]() =sin45°=
=sin45°= ![]() ,
,
∴CP1= ![]() P1D=
P1D= ![]() ,
,
又∵CP1=CQ,
∴CQ= ![]()
(3)解:∵∠P1BE=90°,∠ABC=60°,
∴∠A=∠CBE=30°,
∴AC= ![]() BC,
BC,
由旋转的性质可得:∠ACP1=∠BCE,
∴△AP1C∽△BEC,
∴AP1:BE=AC:BC= ![]() :1,
:1,
设AP1=x,则BE= ![]() x,
x,
在Rt△ABC中,∠A=30°,
∴AB=2BC=2,
∴S△P1BE= ![]() ×
× ![]() x(2﹣x)=﹣
x(2﹣x)=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
故当x=1时,S△P1BE(max)= ![]()
【解析】(1)根据旋转的性质,易证得△B1CQ≌△BCP1,即可得到CQ=CP1。
(2)由(1)结论可知CQ=CP1。要求CQ的长,只需求出CP1的长,添加辅助线,将CP1转化到直角三角形中,作P1D⊥CA于D,根据∠A=30°,可求出P1D的长,然后在Rt△P1DC中,可求出CP1的长,即可得出结论。
(3)根据旋转的性质,先证明△AP1C∽△BEC,得对应边成比例,建立方程,用含x的代数式分别表示出AP1、BE的长,在Rt△ABC中,求出AB的长,即可求出S△P1BE与x的函数关系式,求出顶点坐标,即可得到△P1BE面积的最大值。
【考点精析】根据题目的已知条件,利用二次函数的最值和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.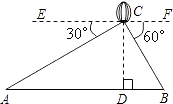
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)同题情景:如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE//AB,∴∠APE+∠PAB=180°,
∴∠APE=180°-∠PAB=180°-130°=50°
∵AB//CD,∴PE//CD.
……
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的解题思路,解答下面的问题:
如图3,AD//BC,当点P在A、B两点之间时,∠ADP=∠α,∠BCP=∠β,则∠CPD,∠α,∠β之间有何数量关系?请说明理由.
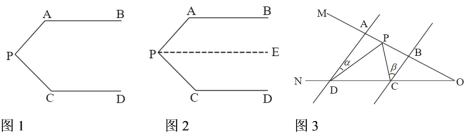
查看答案和解析>>
科目:初中数学 来源: 题型:
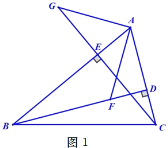
【题目】如图,在△ABC中,BD,CE分别是AC,AB边上的高,在BD上截取BF=AC,延长CE至点G使CG=AB,连接AF,AG.
(1)如图1,求证:AG=AF;
(2)如图2,若BD恰好平分∠ABC,过点G作GH⊥AC交CA的延长线于点H,请直接写出图中所有的全等三角形并用全等符号连接.
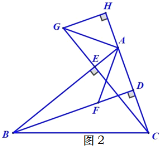
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB,BC于点E,F.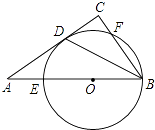
(1)求证:AC是⊙O的切线;
(2)已知AB=5,AC=4,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm
B.7cm
C.12cm
D.17cm或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路去上学,她先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中的折线ABCDE表示小丽和学校之间的距离y(米)与她离家的时间x(分)之间的函数关系.
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.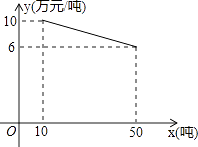
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△![]() ,点C的对应点是直线上的格点
,点C的对应点是直线上的格点![]() .
.
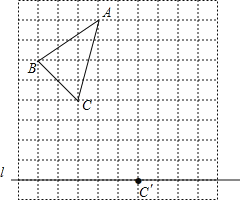
(1)画出△![]() .
.
(2)若连接![]() 、
、![]() ,则这两条线段之间的关系是 .
,则这两条线段之间的关系是 .
(3)试在直线![]() 上画出所有符合题意的格点P,使得由点
上画出所有符合题意的格点P,使得由点![]() 、
、![]() 、
、![]() 、P四点围成的四边形的面积为9.
、P四点围成的四边形的面积为9.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com