
【题目】已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm
B.7cm
C.12cm
D.17cm或7cm
【答案】D
【解析】解:①当弦AB和CD在圆心同侧时,如图1, 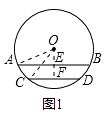
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12﹣5=7cm;
②当弦AB和CD在圆心异侧时,如图2, 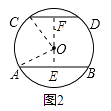
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
所以答案是:D.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
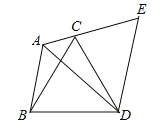
【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题共10分)水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
(3)现需按毛利润的10%交纳各种税费,人工费每日按销售量每千克支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每千克涨价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在横线上和括号内填上推导内容或依据.
如图,已知 ![]() ,
, ![]() ,求证:
,求证: ![]() .
.
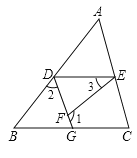
证明: ![]() (已知),
(已知),
![]() ( ),
( ),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
∵![]() (已知),
(已知),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;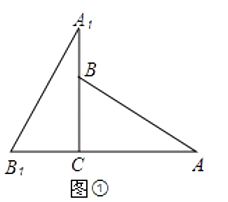
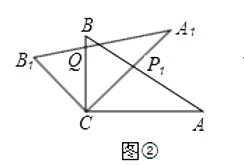
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.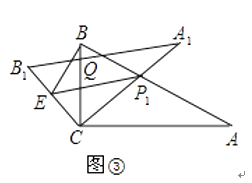
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校区内有甲、乙两块大小一样的长方形地块,地块长30m,宽25m,现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分),余下的部分绿化.现已知ABCD1m,EFGH1m,记甲、乙地块的绿化面积分别为S1、S2,则S1、S2的大小关系是( )

A.S1<S2B.S1=S2C.S1>S2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
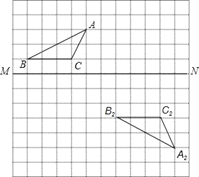
【题目】在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com