Question

【题目】如图(1)，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上的一点，连接BO交AD于点F，OE⊥OB交BC边于点E．

(1)试说明：△ABF∽△COE．

(2)如图(2)，当O为AC边的中点，且时，求的值．

(3)当O为AC边的中点，时，请直接写出的值．

Answer 1

【答案】详见解析； (3)

【解析】

（1）要求证：△ABF∽△COE.只要证明∠BAF=∠C，∠ABF=∠COE即可．
（2）作交BC于H，易证：△OEH∽△OFA，根据相似三角形的对应边的比相等，即可得出所求的值．同理可得（3）

(1)证明：∵AD⊥BC，

∴

∵

∴∠BAF=∠C.

∵OE⊥OB，

∴

∵

∴∠ABF=∠COE.

∴△ABF∽△COE.

(2)过O作AC垂线交BC于H,则OHAB，

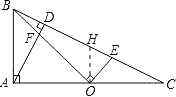
由(1)得∠ABF=∠COE，∠BAF=∠C.

∴∠AFB=∠OEC，

∴∠AFO=∠HEO，

而∠BAF=∠C，

∴∠FAO=∠EHO，

∴△OEH∽△OFA，

∴OF:OE=OA:OH

又∵O为AC的中点,OHAB.

∴OH为△ABC的中位线，

∴

而

∴OA:OH=2:1，

∴OF:OE=2:1,即

(3)