
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”(例如圆的直径就是它的“面径”).已知等边三角形的边长为4,则它的“面径”长x的取值范围是 _.
【答案】2![]() (或介于2
(或介于2![]() 和2
和2![]() 之间的任意两个实数).
之间的任意两个实数).
【解析】
试题分析:本题考查了等边三角形的性质,读懂题意,弄明白面径的定义,并准确判断出等边三角形的最短与最长的面径是解题的关键.根据等边三角形的性质,
(1)最长的面径是等边三角形的高线;
(2)最短的面径平行于三角形一边,最长的面径为等边三角形的高,然后根据相似三角形面积的比等于相似比的平方求出最短面径.
如图,

(1)等边三角形的高AD是最长的面径,
AD=![]() ×4=2
×4=2![]() ;
;
(2)当EF∥BC时,EF为最短面径,
此时,(![]() )2=
)2=![]() ,
,
即![]() =
=![]() ,
,
解得EF=2![]() .
.
所以,它的面径长可以是2![]() (或介于2
(或介于2![]() 和2
和2![]() 之间的任意两个实数).
之间的任意两个实数).
故答案为2![]() (或介于2
(或介于2![]() 和2
和2![]() 之间的任意两个实数).
之间的任意两个实数).


科目:初中数学 来源: 题型:
【题目】如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行____________分钟可使渔船到达离灯塔距离最近的位置.
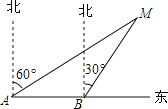
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P在四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为( )
A.(﹣3,﹣2)
B.(3,﹣2)
C.(2,3)
D.(2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,AB=BC, BO是AC边上的中线,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E,


(1)求证:△BPO≌△PDE.
(2)若PB平分∠ABO,其余条件不变.求证:AP=CD.
(先将图形补充完整,然后再证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.

(1)求证:四边形ABCD是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么△DCB的面积是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为_____.
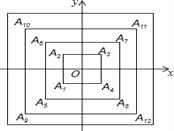
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
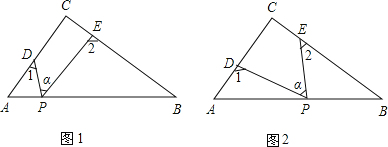
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
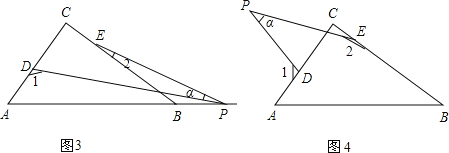
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com