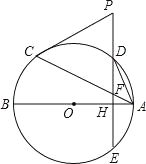
【题目】如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O于E，交AB于H，交AC于F．P是ED延长线上一点且PC=PF．

（1）求证：PC是⊙O的切线；

（2）若点D是劣弧AC的中点，OH=1，AH=2，求弦AC的长．

参考答案：

【答案】（1）证明见解析；

（2）AC=4．

【解析】

试题分析：（1）根据等腰三角形的性质和直角三角形两锐角互余的性质，证得∠PCF+∠AC0=90°，即OC⊥PC，即可证得结论；

（2）先根据勾股定理求出DH，再通过证明△OGA≌△OHD，得出AC=2AG=2DH，求出弦AC的长．

试题解析：（1）连接OC，∵OA=OC，∴∠ACO=∠OAC，∵PC=PF，

∴∠PCF=∠PFC，∵DE⊥AB，∴∠OAC+∠AFH=90°，

∵∠PDF=∠AFH，

∴∠PFC+∠OAC=90°，

∴∠PCF+∠AC0=90°，

即OC⊥PC，

∴PC是⊙O的切线；

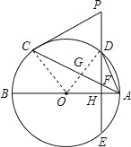
（2）连接OD交AC于G．

∵OH=1，AH=2，

∴OA=3，即可得OD=3，

∴DH===2．

∵点D在劣弧AC中点位置，∴AC⊥DO，∴∠OGA=∠OHD=90°，

在△OGA和△OHD中，

，

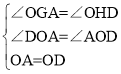∴△OGA≌△OHD（AAS），

∴AG=DH，

∴AC=4．

关闭