
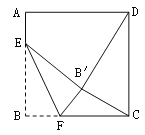
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
【答案】(1)证明见解析;(2)![]() ;(3)△CB′F周长的最小值为
;(3)△CB′F周长的最小值为![]() .
.
【解析】(1)利用正方形的性质即可证得结论;(2)运用翻折的性质在Rt△B′MF中运用勾股定理BF的长;(3)根据折叠的对称性求出△CB′F周长的最小值.
(1)证明:
∵ABCD是正方形,
∴∠B=90°,AB=BC,
∵∠BEF=45°,
∴∠BFE=∠BEF=45°,
∴BE=BF,
∴AE=CF.
(2)如图1,过B′点作GH∥AD,分别交AB、CD于点G、H,则∠B′GE=90°.
∵B′C=B′D,

∴DH=AG=![]() DC=8,
DC=8,
∵AE=3,AB=16,
∴BE=13,
由翻折的性质可得:B′E=BE=13.
∴ EG=AG﹣AE=8﹣3=5,
∴ B′G=![]() ,
,
过B′点作B′M∥BC交BC于点M,
则B′M=BG=8.BM=B′G=12,
设BF= ![]() ,则B′F=BF=
,则B′F=BF= ![]() ,FM=12﹣
,FM=12﹣![]() ,
,
在Rt△B′MF中,∠B′MF=90°,
∴ B′F2= FM2+ B′M2,
即![]() ,
,
解得: ![]() ,即BF =
,即BF =![]() .
.
(3)如图2.
∵FB′+ FC=BC=16,
∴当CB′最小时,△CB′F的周长也最小,

而当C、B′、E三点共线时,CB′取最小值,
此时CB′=CE-EB′=![]() ,
,
∴△CB′F周长的最小值为![]() .
.
或∵FB′+ FC=BC=16,
∴当CB′最小时,△CB′F的周长也最小,
当∠CB′F=90°时,CB′最小,
而这时C、B′、E三点共线,
此时CB′=CE-EB′=![]() ,
,
∴△CB′F周长的最小值为![]() .
.
“点睛”本题考查了正方形的性质、翻折的性质、折叠的对称性,灵活运用性质是解题的关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】In right Fig.,if the length of the segment AB is 1,M is the midpoint of the segment AB,and point C divides the segment MB into two parts such that MC:CB=1:2,then the length of AC is 。
(英汉词典:length 长度;segment 线段;midpoint 中点;divides…into 分为,分成)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3
B.三边长分别为5,12,14
C.三边长之比为3:4:5
D.三边长分别为1, ![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( ) 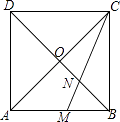
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E. 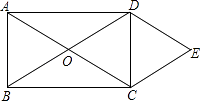
(1)求证:四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是边BC所在的直线上的动点(点D不与B、C重合),过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)求证:AF=DE;
(2)若AC=5,DE=6,则DF= .
(3)试探究:D在不同位置时,DE,DF,AC具有怎样的数量关系,直接写出结论:
①当点D在线段BC上时,关系是:;
②当点D在线段BC延长线上时,关系是:;
③当点D在线段CB延长线上时,关系是:;
(4)请选择(3)中你探究获得的其中一个结论证明之.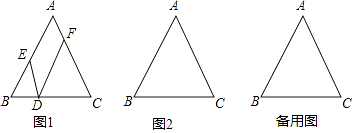
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com