
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E. 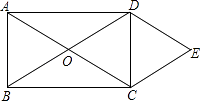
(1)求证:四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.
【答案】
(1)证明:∵DE∥OC,CE∥OD,
∵四边形OCED是平行四边形.
∴OC=DE,OD=CE
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴CE=OC=BO=DE.
∴四边形OCED是菱形
(2)解:如图,连接OE.
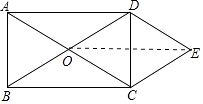
在Rt△ADC中,AD=4,CD=3
由勾股定理得,AC=5∴OC=2.5
∴C菱形OCED=4OC=4×2.5=10,
在菱形OCED中,OE⊥CD,又∵OE⊥CD,
∴OE∥AD.
∵DE∥AC,OE∥AD,
∴四边形AOED是平行四边形,
∴OE=AD=4.
∴S菱形OCED= ![]() .
.
【解析】(1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,(2)根据S△ODC= ![]() S矩形ABCD以及四边形OCED的面积=2S△ODC即可解决问题.
S矩形ABCD以及四边形OCED的面积=2S△ODC即可解决问题.


科目:初中数学 来源: 题型:
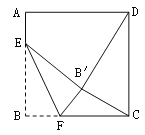
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为 . 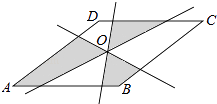
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题. 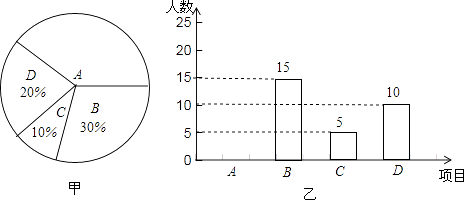
(1)样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论: ①S1+S2=S3+S4;②S2+S4=S1+S3;③若S3=2S1 , 则S4=2S2;④若S1=S2 , 则P点在矩形的对角线上.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).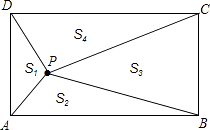
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com