
����Ŀ���ڡ�ABC�У�AB=AC����D�DZ�BC���ڵ�ֱ���ϵĶ��㣨��D����B��C�غϣ�������D��DE��AC��ֱ��AB�ڵ�E��DF��AB��ֱ��AC�ڵ�F��
��1����֤��AF=DE��
��2����AC=5��DE=6����DF= ��
��3����̽����D�ڲ�ͬλ��ʱ��DE��DF��AC����������������ϵ��ֱ��д�����ۣ�
�ٵ���D���߶�BC��ʱ����ϵ�ǣ���
�ڵ���D���߶�BC�ӳ�����ʱ����ϵ�ǣ���
�۵���D���߶�CB�ӳ�����ʱ����ϵ�ǣ���
��4����ѡ��3������̽����õ�����һ������֤��֮��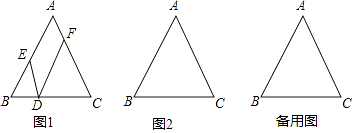
���𰸡�
��1��
֤������DE��AC��DF��AB��
���ı���AEDF��ƽ���ı��Σ�
��AF=DE
��2��1��11
��3��DE+DF=AC��DE��DF=AC��DF��DE=AC
��4��
�⣺ѡ�٣�ͬ��1���ã��ı���AEDF��ƽ���ı��Σ�
��DF=AE��
��AB=AC��
���ABC=��ACB��
��DF��AB��
���FDC=��ABC��
���FDC=��ACB��
��DF=CF��
��AF+CF=AC��
��DE+DF=AC
����������2���⣺�����������
�� ��ͼ2��ʾ��
ͬ��1���ã��ı���AEDF��ƽ���ı��Σ�
��DF=AE��
��AB=AC��
���ABC=��ACB��
��DE��AC��
���BDE=��ACB��
���ABC=��BDE��
��BE=DE=6��
��DF=AE=BE��AB=6��5=1��
����ͼ2��ʾ��ͬ�ٵã�DF=AE��BE=DE=6��
��DF=AE=6+5=11��
����������DF�ij�Ϊ1��11��
���Դ��ǣ�1��11��
����3�����ɣ�1����2���ã�DE=AF��DF=CF��
��AC=AF+CF��
��DE+DF=AC��
���Դ��ǣ�DE+DF=AC��
���ɣ�1����2���ã�DE=AF��DF=CF��
��AC=AF��CF��
��DE��DF=AC��
���Դ��ǣ�DE��DF=AC��
���ɣ�1����2���ã�DE=AF��DF=AE��BE=DE��
��AB=AE��BE��AC=AB��
��DF��DE=AC��
���Դ��ǣ�DF��DE=AC��
�����㾫�������ڱ��⿼���ƽ���ı��ε����ʣ���Ҫ�˽�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�ֲ��ܵó���ȷ�𰸣�


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
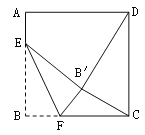
����Ŀ����ͼ��������ABCD�ı߳���16����E�ڱ�AB�ϣ�AE=3������F�ڱ�BC�ϣ��Ҳ����B��C�غϣ�����EBF��EF�۵����õ���EB��F.
��1������BEF=45��ʱ����֤��CF=AE��
��2����B��D=B��Cʱ����BF�ij���
��3�����CB��F�ܳ�����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�˻������У��������ִ�Ⱦ����64�˻������У���ÿ�ִ�Ⱦ��ƽ��һ���˴�Ⱦ��������
A.5��B.6��C.7��D.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ����������ɫ�����������������A����ë��B������C��ƹ����D����������������Ŀ��Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ��ÿ��ֻѡȡһ�֣��������ȡ�˲���ѧ�����е��飬���������������ס�����ʾ��ͳ��ͼ��������ͼ����Ϣ����������⣮ 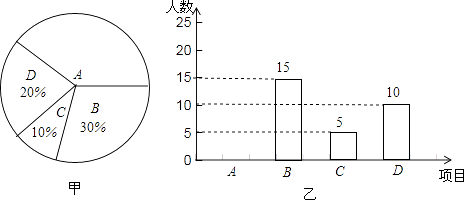
��1����������ϲ��A��Ŀ��������ռ�İٷֱ�Ϊ �� ����������ͳ��ͼ�ж�Ӧ��Բ�ĽǶ������ȣ�
��2���������ͳ��ͼ����������
��3������У��ѧ��3000�ˣ��������������ȫУ��ϲ�������ѧ������Լ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���kx2+��k+3��x+2��0����֤������kȡ�κη���ʵ�����÷��̶�����������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC����D�ڱ�AB�ϣ�����CD�����߶�CD�Ƶ�C˳ʱ����ת90����CEλ�ã�����AE��
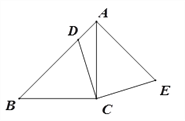
��1����֤��AB��AE��
��2����![]() ����֤���ı���ADCEΪ�����Σ�
����֤���ı���ADCEΪ�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ǰ尴��ͼ��ʾ�ķ�ʽ���ã������н��۲���ȷ���ǣ� �� 
A.��1=��3
B.�����2=30�㣬����AC��DE
C.�����2=30�㣬����BC��AD
D.�����2=30�㣬���С�4=��C
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�Ǿ���ABCD�ڵ�����һ�㣬����PA��PB��PC��PD���õ���PAB����PBC����PCD����PDA�������ǵ�����ֱ���S1��S2��S3��S4 �� �������½��ۣ� ��S1+S2=S3+S4����S2+S4=S1+S3������S3=2S1 �� ��S4=2S2������S1=S2 �� ��P���ھ��εĶԽ����ϣ�
������ȷ�Ľ��۵����������������ȷ���۵���Ŷ����ں����ϣ���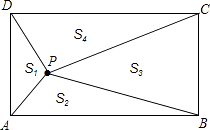
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��P�Ǿ���ABCD�ڵ�����һ�㣬����PA��PB��PC��PD���õ���PAB����PBC����PCD����PDA�������ǵ�����ֱ���S1��S2��S3��S4 �� �������½��ۣ���S1+S4=S2+S3����S2+S4=S1+S2������S3=2S1 �� ��S4=2S2������S1=S2 �� ��S3=S4 �� ������ȷ���۵������ �� 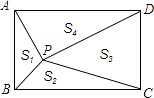
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com