
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
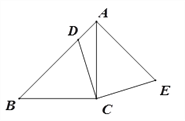
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
【答案】证明:(1)∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴∠DCE=90°,CD=CE,
∵∠ACB=90°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中
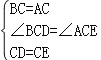 ,
,
∴△BCD≌△ACE,
∴∠B=∠CAE=45°,
∴∠BAE=45°+45°=90°,
∴AB⊥AE;
(2)∵![]() ,
,
而BC=AC,
∴![]() ,
,
∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,
∴四边形ADCE为矩形,
∵CD=CE,
∴四边形ADCE为正方形
【解析】试题分析:(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论;
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形.
解答:证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE,
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE,
在△BCD和△ACE中,∵BC=AC,∠BCD=∠ACE,CD=CE,∴△BCD≌△ACE,
∴∠B=∠CAE=45°,∴∠BAE=45°+45°=90°,∴AB⊥AE;
(2)∵BC2=ADAB,而BC=AC,∴AC2=ADAB,
∵∠DAC=∠CAB,∴△DAC∽△CAB,∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形,
∵CD=CE,∴四边形ADCE为正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( ) 
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是边BC所在的直线上的动点(点D不与B、C重合),过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)求证:AF=DE;
(2)若AC=5,DE=6,则DF= .
(3)试探究:D在不同位置时,DE,DF,AC具有怎样的数量关系,直接写出结论:
①当点D在线段BC上时,关系是:;
②当点D在线段BC延长线上时,关系是:;
③当点D在线段CB延长线上时,关系是:;
(4)请选择(3)中你探究获得的其中一个结论证明之.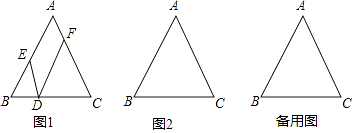
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( ) 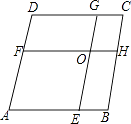
A.6.5
B.6
C.5.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )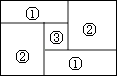
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=2AD.
(1)作AE平分∠BAD交DC于E(尺规作图,保留作图痕迹);
(2)在(1)的条件下,连接BE,判定△ABE的形状(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简:
(1)(﹣ ![]() )×(﹣12)
)×(﹣12)
(2)(﹣3)2÷(2 ![]() )﹣4×(﹣
)﹣4×(﹣ ![]() )2
)2
(3)x2y﹣3×( ![]() xy2﹣
xy2﹣ ![]() yx2)+y2x,其中x=﹣2,y=1.
yx2)+y2x,其中x=﹣2,y=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com