【题目】如图，已知∠XOY=90°，等边三角形PAB的顶点P与O点重合，顶点A是射线OX上的一个定点，另一个顶点B在∠XOY的内部．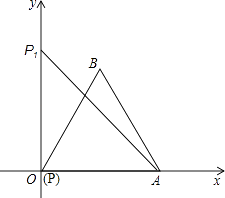
（1）当顶点P在射线OY上移动到点P1时，连接AP1 ， 请用尺规作图；在∠XOY内部作出以AP1为边的等边△AP1B1（要求保留作图痕迹，不要求写作法和证明）；
（2）设AP1交OB于点C，AB的延长线交B1P1于点D．求证：△ABC∽△AP1D；
（3）连接BB1 ， 求证：∠ABB1=90°．

参考答案：

【答案】
（1）解：等边三角形作图所如下；


（2）∵△PAB、△P1AB1是等边三角形，

∴∠ABC=∠AP1D=60°，

又∵∠BAC=∠P1AD，

∴△ABC∽△AP1D．


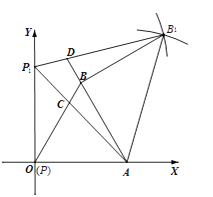
（3）证明：

∵△PAB、△P1AB1是等边三角形，

∴∠BAP=∠P1AB1=60°，AB=AP，AB1=AP1．

∴∠BA B1=∠P1AP．

∴△BA B1≌△P1AP（SAS）．

∴∠AB B1=∠P1 PA=90°．


【解析】（1）分别以A、P1为圆心，AP1长为半径画弧，两弧交于B1点，△AP1B1即为所求；（2）欲证△ABC∽△AP1D，必须有两组角相等，∠BAC=∠P1AD为一个公共角，又因为△PAB和△P1AB1都是正三角形，所以有∠ABC=∠AP1D=60°所以△ABC∽△AP1D；（3）有（1）（2）可知AO=AB，AP1=AB1 ， ∠PAB=∠P1AB1=60°，所以有∠OAP1=∠BAB1=60°﹣∠CAB，因此根据边角边公式可证△OAP1≌△BAB1 ， 因此可得∠ABB1=∠AOP1=90°
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．

关闭