练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

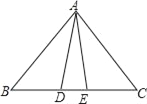
    【题目】如图，已知△ABE≌△ACD．

    （1）如果BE=6，DE=2，求BC的长；

    （2）如果∠BAC=75°，∠BAD=30°，求∠DAE的度数．

    【答案】（1）10；（2）15°

    【解析】

    （1）根据全等三角形的性质，可得出BE=CD，根据BE=6，DE=2，得出CE=4，从而得出BC的长；

    （2）根据全等三角形的性质可得出∠BAE=∠CAD，即可得出∠BAD=∠CAE，计算∠CAD﹣∠CAE即得出答案．

    解：（1）∵△ABE≌△ACD，

    ∴BE=CD，∠BAE=∠CAD，

    又∵BE=6，DE=2，

    ∴EC=DC﹣DE=BE﹣DE=4，

    ∴BC=BE+EC=10；

    （2）∠CAD=∠BAC﹣∠BAD=75°﹣30°=45°，

    ∴∠BAE=∠CAD=45°，

    ∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC=90°，AB=AC=6，D为BC的中点．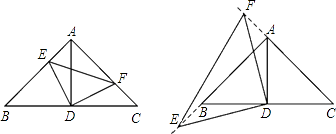
    （1）若E、F分别是AB、AC上的点，且AE=CF，求证：△AED≌△CFD；
    （2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；
    （3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠XOY=90°，等边三角形PAB的顶点P与O点重合，顶点A是射线OX上的一个定点，另一个顶点B在∠XOY的内部．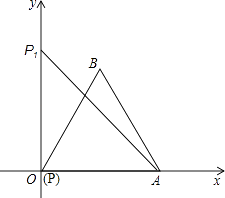
    （1）当顶点P在射线OY上移动到点P1时，连接AP1 ， 请用尺规作图；在∠XOY内部作出以AP1为边的等边△AP1B1（要求保留作图痕迹，不要求写作法和证明）；
    （2）设AP1交OB于点C，AB的延长线交B1P1于点D．求证：△ABC∽△AP1D；
    （3）连接BB1 ， 求证：∠ABB1=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边AB在数轴上，数轴上点A表示的数为-1，正方形ABCD的面积为16．

    （1）数轴上点B表示的数为 ；

    （2）将正方形ABCD沿数轴水平移动，移动后的正方形记为，移动后的正方形与原正方形ABCD重叠部分的面积记为S．

    ① 当S =4时，画出图形，并求出数轴上点表示的数；

    ② 设正方形ABCD的移动速度为每秒2个单位长度，点E为线段的中点，点F在线段上，且. 经过秒后，点E，F所表示的数互为相反数，直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

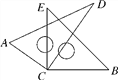
    【题目】如图，将两块直角三角尺的顶点叠放在一起．

    (1)若∠DCE＝35°，求∠ACB的度数；

    (2)若∠ACB＝140°，求∠DCE的度数；

    (3)猜想∠ACB与∠DCE的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校为了推动球类运动的普及，成立多个球类运动社团，为此，学生会采取抽样调查的方法，从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好（要求每位同学只能选择其中一种自己喜欢的球类运动），并将调查结果绘制成了如下条形统计图和扇形统计图（不完整）．请你根据图中提供的信息，解答下列问题：

    （1）本次抽样调查，共调查了 名学生；

    （2）请将条形统计图和扇形统计图补充完整；

    （3）若该学校共有学生1800人，根据以上数据分析，试估计选择排球运动的同学约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

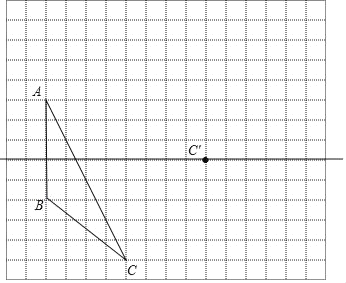
    【题目】如图，方格纸中每个小正方形的边长都为1，在方格纸中将三角形ABC经过一次平移后得到三角形A'B' C′，图中标出了点C的对应点C'．

    （1）请画出平移后的三角形A'B'C′；

    （2）连接AA′，CC′，则这两条线段之间的关系是　 　；

    （3）三角形A'B'C'的面积为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东30°、西北（即北偏西45°）方向上又分别发现了客轮B和海岛C．

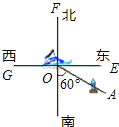
    （1）仿照表示灯塔方位的方法，分别画出表示客轮B和海岛C方向的射线OB，OC（不写作法）；

    （2）若图中有一艘渔船D，且∠AOD的补角是它的余角的3倍，画出表示渔船D方向的射线OD，则渔船D在货轮O的 （写出方位角）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中有Rt△ABC，∠A=90°，AB=AC，A（﹣2，0）、B（0，1）、C（d，2）．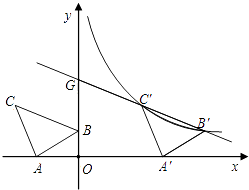

    （1）求d的值；
    （2）将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上．请求出这个反比例函数和此时的直线B′C′的解析式；
    （3）在（2）的条件下，直线BC交y轴于点G．问是否存在x轴上的点M和反比例函数图象上的点P，使得四边形PGMC′是平行四边形？如果存在，请求出点M和点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案