
【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为-1,正方形ABCD的面积为16.
(1)数轴上点B表示的数为 ;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为![]() ,移动后的正方形
,移动后的正方形![]() 与原正方形ABCD重叠部分的面积记为S.
与原正方形ABCD重叠部分的面积记为S.
① 当S =4时,画出图形,并求出数轴上点![]() 表示的数;
表示的数;
② 设正方形ABCD的移动速度为每秒2个单位长度,点E为线段![]() 的中点,点F在线段
的中点,点F在线段![]() 上,且
上,且![]() . 经过
. 经过![]() 秒后,点E,F所表示的数互为相反数,直接写出
秒后,点E,F所表示的数互为相反数,直接写出![]() 的值.
的值.

【答案】(1)-5;(2)– 4或2;(3)t=4.
【解析】试题分析:(1)、根据正方形的面积得出AB=4,根据点A所表示的数得出点B所表示的数;(2)、①、根据题意得出矩形的一边长为4,要使面积为4,则另一边长为1,然后根据向左移动和向右移动两种情况分别画出图形得出答案;②、用含t的代数式分别表示出点E和点F所表示的数,然后根据互为相反数的两个数的和为零列出方程得出答案.
试题解析:解:(1)、–5;
(2)、∵正方形ABCD的面积为16,∴边长为4.
当S=4时,①若正方形ABCD向左平移,如图1,
重叠部分中的A'B =1,∴AA'=3.
则点A'表示–1–3= – 4.
②若正方形ABCD向右平移,如图2,
重叠部分中的AB'=1,∴AA'=3.
则点A'表示–1+3= 2,∴点A'表示的数为– 4或2.
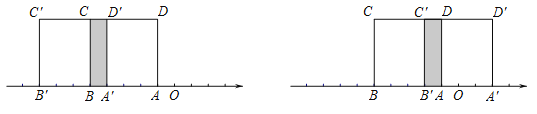
图1 图2
(3)t=4.


科目:初中数学 来源: 题型:
【题目】某市正在进行商业街改造,商业街起点在古民居P的南偏西60°方向上的A处,现已改造至古民居P南偏西30°方向上的B处,A与B相距150m,且B在A的正东方向.为不破坏古民居的风貌,按照有关规定,在古民居周围100m以内不得修建现代化商业街.若工程队继续向正东方向修建200m商业街到C处,则对于从B到C的商业街改造是否违反有关规定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与计算
(1)已知:![]() .
.
求作:在图2中,以OA为一边,在∠AOB的内部作.∠AOC=![]() (要求:直尺和圆规作图,不写作法,保留图痕迹.)
(要求:直尺和圆规作图,不写作法,保留图痕迹.)

(2)过点O分别引射线OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在直角坐标系中的位置如图所示,其中A(﹣3,5),B(﹣5,2),C(﹣1,3),直线l经过点(0,1),并且与x轴平行,△A′B′C′与△ABC关于线1对称.
(1)画出△A′B′C′,并写出△A′B′C′三个顶点的坐标: ;
(2)观察图中对应点坐标之间的关系,写出点P(a,b)关于直线l的对称点P′的坐标: ;
(3)若直线l′经过点(0,m),并且与x轴平行,根据上面研究的经验,写出点Q(c,d)关于直线1′的对称点Q′的坐标: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a= ![]() .其中正确的是( )
.其中正确的是( )
A.②④
B.②③
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上, ![]() =
= ![]() ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y= ![]() 的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于 ![]() ,则k的值是.
,则k的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生最喜爱的球类运动,某初中在全校2000名学生中抽取部分学生进行调查,要求学生只能从“A(篮球)、B(羽毛球)、C(足球)、D(乒乓球)”中选择一种.
(1)小明直接在八年级学生中随机调查了一些同学.他的抽样是否合理?请说明理由.
(2)小王从各年级随机抽取了部分同学进行调查,整理数据,绘制出下列两幅不完整的统计图.请根据图中所提供的信息,回答下列问题:
①请将条形统计图补充完整;
②估计该初中最喜爱乒乓球的学生人数约为 人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com