
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC=6��DΪBC���е㣮 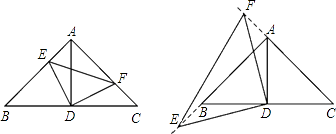
��1����E��F�ֱ���AB��AC�ϵĵ㣬��AE=CF����֤����AED�ա�CFD��
��2������F��E�ֱ��C��A����ͬʱ��������ÿ��1����λ���ȵ��ٶ���CA��AB�˶�������A��Bʱֹͣ�����DEF�����Ϊy��F���˶���ʱ��Ϊx����y��x�ĺ�����ϵʽ��
��3���ڣ�2���������£���F��E�ֱ���CA��AB���ӳ������˶������ʱy��x�ĺ�����ϵʽ��
���𰸡�
��1��֤�����ߡ�BAC=90�� AB=AC=6��DΪBC�е�
���BAD=��DAC=��B=��C=45��
��AD=BD=DC
��AE=CF���AED�ա�CFD��SAS��
��2���⣺�������У�FC=AE=x��
�ߡ�AED�ա�CFD
��S�ı���AEDF=S��AED+S��ADF=S��CFD+S��ADF=S��ADC=9
�� ![]() S�ı���AEDF-
S�ı���AEDF- ![]()
�� ![]() ��
��
��3���⣺�������У�AF=BE=x��6��AD=DB����ABD=��DAC=45��
���DAF=��DBE=135��
���ADF�ա�BDE
��S��ADF=S��BDE
��S��EDF=S��EAF+S��ADB
= ![]()
�� ![]() ��
��

����������1�����õ���ֱ�������ε����ʵõ���BAD=��DAC=��B=��C=45�㣬�����õ�AD=BD=DC��Ϊ֤����AED�ա�CFD�ṩ����Ҫ����������2������S�ı���AEDF=S��AED+S��ADF=S��CFD+S��ADF=S��ADC=9 ���ɵõ�y��x֮��ĺ�����ϵʽ����3���������У�AF=BE=x��6��AD=DB����ABD=��DAC=45��õ���DAF=��DBE=135�㣬�Ӷ��õ���ADF�ա�BDE������ȫ�������������ȵõ�S��ADF=S��BDE�Ӷ��õ�S��EDF=S��EAF+S��ADB����ȷ����������֮��ĺ�����ϵʽ��
�����㾫�������ڱ��⿼��ĵ���ֱ�������Σ���Ҫ�˽����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45����ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC�Ĵ�ֱƽ���߷ֱ�BC�ڵ�E��F��
��1������AEF���ܳ�Ϊ10cm����BC�ij�Ϊ______cm��
��2������EAF=100�㣬���BAC______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֻ������Ѿ���Ϊ����������ʱ�е��������ij���繫˾�����������̻����Ƴ��������ֻ������ļƷѷ�ʽ����ʽA��ÿ����0.1Ԫ�ļ۸�����ʱ��Ʒѣ���ʽB�����»���20Ԫ�⣬����ÿ����0.06Ԫ�ļ۸�����ʱ��Ʒѣ�����ij�ͻ����ֻ�������ʱ��Ϊx���ӣ���������ΪyԪ�� 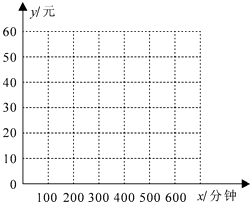
��1���ֱ�д���ÿͻ���A��B���ַ�ʽ��������y��Ԫ����ÿ������ʱ��x�����ӣ��ĺ�����ϵʽ��������ͼ������ϵ�л���������������ͼ��
��2�����ѡ��Ʒѷ�ʽ��ʹ�ÿͻ��������ø����㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڽ�����ҵ�ָ��죬��ҵ������ڹ����P����ƫ��60�㷽���ϵ�A�������Ѹ����������P��ƫ��30�㷽���ϵ�B����A��B���150m����B��A����������Ϊ���ƻ�����ӵķ�ò�������йع涨���ڹ������Χ100m���ڲ������ִ�����ҵ�֣������̶Ӽ���������������200m��ҵ�ֵ�C��������ڴ�B��C����ҵ�ָ����Ƿ�Υ���йع涨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������Ħ�г�ͬʱ�����20km��A��B���س�����������У�ͼ��l1��l2�ֱ��ʾ�ס�������Ħ�г���A�صľ���s��km������ʻʱ��t��h���ĺ�����ϵ��������˵���������
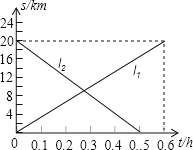
A. ��Ħ�г����ٶȽϿ�
B. ����0.3Сʱ��Ħ�г���ʻ��A��B���ص��е�
C. ����0.25Сʱ��Ħ�г�����
D. ����Ħ�г�����A��ʱ����Ħ�г�����A��![]() km
km
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���û�������ͼ�ķ�ʽ����ʽ�����Σ���һ��ͼ����3���������ڶ���ͼ����9��������������ͼ����18��������......����������ȥ����9��ͼ����_____��������
 ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���A=50�㣬BC=6����BCΪֱ���İ�ԲO��AB��AC�ֱ��ڵ�D��E����ͼ����Ӱ�������֮�͵�������������У���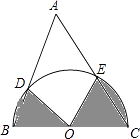
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
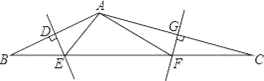
����Ŀ����ͼ�����
��1����֪��![]() ��
��
��������ͼ2�У���OAΪһ�ߣ��ڡ�AOB���ڲ�������AOC��![]() ��Ҫ��ֱ�ߺ�Բ����ͼ����д����������ͼ�ۼ�����
��Ҫ��ֱ�ߺ�Բ����ͼ����д����������ͼ�ۼ�����

��2������O�ֱ�������OA��OB��OC���ҡ�AOB=65������BOC=30�������AOC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABE�ա�ACD��
��1�����BE=6��DE=2����BC�ij���
��2�������BAC=75�㣬��BAD=30�������DAE�Ķ�����
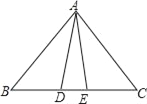
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com