
【题目】某中学计划购进甲、乙两种学具,已知一件甲种学具的进价与一件乙种学具的进价的和为40元,用90元购进甲种学具的件数与用150元购进乙种学具的件数相同.
![]() 求每件甲种、乙种学具的进价分别是多少元?
求每件甲种、乙种学具的进价分别是多少元?
![]() 该学校计划购进甲、乙两种学县共100件,此次进货的总资金不超过2000元,求最少购进甲种玩具多少?
该学校计划购进甲、乙两种学县共100件,此次进货的总资金不超过2000元,求最少购进甲种玩具多少?
【答案】(1) 甲,乙两种学具分别是15元![]() 件,25元
件,25元![]() 件;(2) 甲种学具最少购进50个.
件;(2) 甲种学具最少购进50个.
【解析】
. (1)设甲种学具进价x元/件,则乙种学具进价为(40-x)元/件,根据一件甲种学具的进价与一件乙种学具的进价的和为40元,用90元购进甲种学具的件数与用150元购进乙种学具的件数相同可列方程求解.(2)设购进甲种学具y件,则购进乙种学具(100-y)件,根据学校决定此次进货的总资金不超过2000元,可列出不等式求解;
![]() 设甲种学具进价x元
设甲种学具进价x元![]() 件,则乙种学具进价为
件,则乙种学具进价为![]() 元
元![]() 件,
件,
可得:![]()
解得:![]() ,
,
经检验![]() 是原方程的解.
是原方程的解.
故![]() .
.
答:甲,乙两种学具分别是15元![]() 件,25元
件,25元![]() 件;
件;
![]() 设购进甲种学具y件,则购进乙种学具
设购进甲种学具y件,则购进乙种学具![]() 件,
件,
![]()
解得:![]() .
.
答:甲种学具最少购进50个;


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( ) 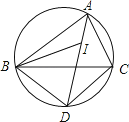
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上,点 A 的初始位置表示的数为 1,现点 A 做如下移动:第 1 次点 A 向左移动 3 个单位长度至点 A1,第 2 次从点 A1 向右移动 6 个单位长度至点 A2,第 3 次从点 A2 向左移动 9 个单位长度至点 A3,…,按照这种移动方式进行下去,点 A4 表示的数,是__________ ,如果点 An 与原点的距离不小于 20, 那么 n 的最小值是________________ .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.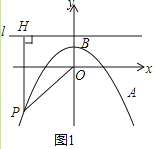
(1)求抛物线的解析式,并写出其顶点B的坐标;
(2)①当P点运动到A点处时,计算:PO= , PH= , 由此发现,POPH(填“>”、“<”或“=”);
②当P点在抛物线上运动时,猜想PO与PH有什么数量关系,并证明你的猜想;
(3)如图2,设点C(1,﹣2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.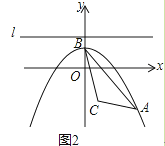
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com