
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.
![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
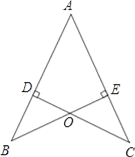
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购进甲、乙两种学具,已知一件甲种学具的进价与一件乙种学具的进价的和为40元,用90元购进甲种学具的件数与用150元购进乙种学具的件数相同.
![]() 求每件甲种、乙种学具的进价分别是多少元?
求每件甲种、乙种学具的进价分别是多少元?
![]() 该学校计划购进甲、乙两种学县共100件,此次进货的总资金不超过2000元,求最少购进甲种玩具多少?
该学校计划购进甲、乙两种学县共100件,此次进货的总资金不超过2000元,求最少购进甲种玩具多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数 a、b、c 在数轴上的位置如图所示:
(1)比较 a、|b|、c 的大小(用“<”连接);
(2)若 m=|a+b|﹣|b﹣1|﹣|a﹣c|,求 1﹣2013(m+c)2013 的值;
(3)若 a=﹣2,b=﹣3,c=![]() ,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com