
【题目】有理数 a、b、c 在数轴上的位置如图所示:
(1)比较 a、|b|、c 的大小(用“<”连接);
(2)若 m=|a+b|﹣|b﹣1|﹣|a﹣c|,求 1﹣2013(m+c)2013 的值;
(3)若 a=﹣2,b=﹣3,c=![]() ,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
![]()
【答案】(1)a<c<|b|;(2)2014;(3) 0 或 2.
【解析】
(1)根据数轴可得 b<0,因此|b|=﹣b,在数轴上表示出﹣b 的位置, 再根据数轴上的数,左边的数总比右边的小可得答案;
(2)首先根据 a、b、c 的位置得到 a+b<0,b﹣1<0,a﹣c<0,然后再把 m=|a+b|﹣|b﹣1|﹣|a﹣c|化简可得 m+c=﹣1,再代入计算出代数式的值即可;
(3)设 P 点对应的有理数为 x,然后分情况讨论:①当点 P 在点 A 的左边时;
②当点 P 在点A 和点 C 之间时;③当点 P 在点 C 的右边时.
(1)如图所示:
a<c<|b|;
(2)由 a、b、c 在数轴上的位置知:a+b<0,b﹣1<0,a﹣c<0, 所以 m=﹣(a+b)+(b﹣1)+(a﹣c),
=﹣a﹣b+b﹣1+a﹣c,
=﹣1﹣c,
所以 m+c=﹣1,
即 1﹣2013(m+c)2013=1﹣2013(﹣1)2013=1+2013=2014;
(3)存在.设 P 点对应的有理数为 x.
①当点 P 在点 A 的左边时,有﹣2﹣x=3(![]() ﹣x),解之得:x=2(不合条件,舍去),
﹣x),解之得:x=2(不合条件,舍去),
②当点 P 在点 A 和点 C 之间时,有 x﹣(﹣2)=3(![]() ﹣x),解之得:x=0,
﹣x),解之得:x=0,
③当点 P 在点C 的右边时,有 x﹣(﹣2)=3 (x﹣![]() ),解之得:x=2,
),解之得:x=2,
综上所述,满足条件的 P 点对应的有理数为 0 或 2.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上,点 A 的初始位置表示的数为 1,现点 A 做如下移动:第 1 次点 A 向左移动 3 个单位长度至点 A1,第 2 次从点 A1 向右移动 6 个单位长度至点 A2,第 3 次从点 A2 向左移动 9 个单位长度至点 A3,…,按照这种移动方式进行下去,点 A4 表示的数,是__________ ,如果点 An 与原点的距离不小于 20, 那么 n 的最小值是________________ .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b与反比例函数y= ![]() (x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点. 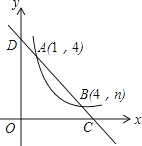
(1)m= , n=;若M(x1 , y1),N(x2 , y2)是反比例函数图象上两点,且0<x1<x2 , 则y1y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于
的小数部分我们不可能全部地写出来,但是由于![]() ,所以
,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,所得的差就是其小数部分
减去其整数部分1,所得的差就是其小数部分![]() ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:
![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
![]() 整数部分是______,小数部分是______;
整数部分是______,小数部分是______;
![]() 若设
若设![]() 整数部分是x,小数部分是y,求
整数部分是x,小数部分是y,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有名学生参加;
(2)直接写出表中a= , b=;
(3)请补全下面相应的频数分布直方图;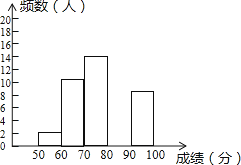
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com