练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，菱形ABCD的对角线AC，BD相交于O，点E，F分别是AD，DC的中点，已知OE=，EF=3，求菱形ABCD的周长和面积．

    【答案】20，24

    【解析】

    首先由菱形ABCD的对角线AC，BD相交于O，点E，F分别是AD，DC的中点，根据直角三角形斜边上的中线等于斜边的一半，可求得AD的长，由三角形中位线定理可求得AC的长，进而可求出菱形的周长，再求出BD的长即可求出菱形的面积．

    ∵菱形ABCD的对角线AC，BD相交于点O，∴AC⊥BD，OA=OC，OB=OD，

    ∵点E，F分别是AD，DC的中点，∴OE=AD，EF=AC，

    ∵OE=2.5，EF=3，∴AD=5，AC=6，∴菱形ABCD的周长为：4×5=20；

    ∵AO=AC=3，AD=5，∴DO==4，∴BD=2DO=8，∴菱形ABCD的面积=ACBD=24．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有理数a，b，c在数轴上的位置如图所示，且|a|=|c|．

    （1）若|a+c|+|b|=2，求b的值；

    （2）用“＞”从大到小把a，b，﹣b，c连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列文字：

    我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如由图1可以得到（a+2b）（a+b）=a2+3ab+2b2．请解答下列问题：

    （1）写出图2中所表示的数学等式_____；

    （2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；

    （3）图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片，

    ①请按要求利用所给的纸片拼出一个几何图形，并画在图3所给的方框中，要求所拼出的几何图形的面积为2a2+5ab+2b2，

    ②再利用另一种计算面积的方法，可将多项式2a2+5ab+2b2分解因式．即2a2+5ab+2b2=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系xOy中，抛物线y=ax2+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．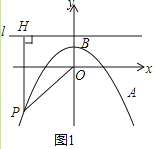
    （1）求抛物线的解析式，并写出其顶点B的坐标；
    （2）①当P点运动到A点处时，计算：PO= ， PH= ， 由此发现，POPH（填“＞”、“＜”或“=”）；
    ②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想；
    （3）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．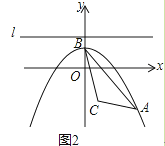

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为x（分），且50≤x＜100，将其按分数段分为五组，绘制出以下不完整表格：

    组别

    成绩x（分）

    频数（人数）

    频率

    一

    50≤x＜60

    2

    0.04

    二

    60≤x＜70

    10

    0.2

    三

    70≤x＜80

    14

    b

    四

    80≤x＜90

    a

    0.32

    五

    90≤x＜100

    8

    0.16

    请根据表格提供的信息，解答以下问题：
    （1）本次决赛共有名学生参加；
    （2）直接写出表中a= ， b=；
    （3）请补全下面相应的频数分布直方图；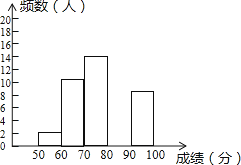

    （4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个两位数恰等于它的各位数字之和的倍，则这个两位数称为“巧数”．不是“巧数”的两位数有______个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】折叠三角形纸片ABC，使点A落在BC边上的点F，且折痕DE∥BC，若∠A=75°，∠C=60°，则∠BDF=____________________________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS，下面四个结论：①AS=AR；②QP∥AR；③△BRP≌△QSP；④AP垂直平分RS．其中正确结论的序号是 （请将所有正确结论的序号都填上）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列四组线段中，可以组成直角三角形的是（　　）

    A. 4，5，6 B. 3，4，5 C. 5，6，7 D. 1，，3

    查看答案和解析>>

    同步练习册答案