
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

【答案】①②③④
【解析】
根据角平分线性质即可推出①,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP//AB即可;在Rt△BRP和Rt△QSP中,只有PR=PS,无法判断△BRP≌△QSP;连接RS,与AP交于点D,先证△ARD≌△ASD,则RD=SD,∠ADR=∠ADS=90°.
①∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,
![]() ,
,
∴Rt△ARP≌Rt△ASP(HL),
∴AR=AS,∴①正确;
②∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP//AR,∴②正确;
③在Rt△BRP和Rt△QSP中,只有PR=PS,
不满足三角形全等的条件,故③错误;
④如图,连接RS,与AP交于点D,
在△ARD和△ASD中,
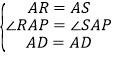 ,
,
∴△ARD≌△ASD,
∴RD=SD,∠ADR=∠ADS=90°,
所以AP垂直平分RS,故④正确,
故答案为:①②④.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
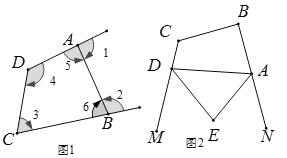
【题目】(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小军两人一起做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于他们各自选择的数,就在做一次上述游戏,直至决出胜负.若小军事先选择的数是5,用列表或画树状图的方法求他获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com