
【题目】若一个两位数恰等于它的各位数字之和的![]() 倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个.
倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个.
【答案】86
【解析】
首先根据题意这个两位数为![]() ,即可得到方程:10x+y=4(x+y),化简得y=2x,又由x,y是不为0的一位数,分析得到这样的“巧数”有4个,即可求得不是“巧数”的两位数的个数.
,即可得到方程:10x+y=4(x+y),化简得y=2x,又由x,y是不为0的一位数,分析得到这样的“巧数”有4个,即可求得不是“巧数”的两位数的个数.
设这个两位数为![]() ,
,
∵这个两位数恰等于它的各位数字之和的4倍,
∴10x+y=4(x+y),
即y=2x,
∵x,y是不为0的一位数,
∴x<5,
∴当x=1时,y=2,则此两位数为12;
当x=2时,y=4,则此两位数为24;
当x=3时,y=6,则此两位数为36;
当x=4时,y=8,则此两位数为48;
∴这样的“巧数”有4个,
∵两位数共有90个,
∴不是“巧数”的两位数的个数是:904=86(个).
故答案为:86.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足 ![]() ,求实数p的值.
,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=﹣x2+bx+c的图象过点A(3,0),B(0,4)两点,动点P从A出发,在线段AB上沿A→B的方向以每秒2个单位长度的速度运动,过点P作PD⊥y于点D,交抛物线于点C.设运动时间为t(秒).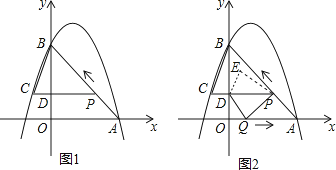
(1)求二次函数y=﹣x2+bx+c的表达式;
(2)连接BC,当t= ![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图2,动点P从A出发时,动点Q同时从O出发,在线段OA上沿O→A的方向以1个单位长度的速度运动.当点P与B重合时,P、Q两点同时停止运动,连接DQ,PQ,将△DPQ沿直线PC折叠得到△DPE.在运动过程中,设△DPE和△OAB重合部分的面积为S,直接写出S与t的函数关系及t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com