
【题目】如图1,二次函数y=﹣x2+bx+c的图象过点A(3,0),B(0,4)两点,动点P从A出发,在线段AB上沿A→B的方向以每秒2个单位长度的速度运动,过点P作PD⊥y于点D,交抛物线于点C.设运动时间为t(秒).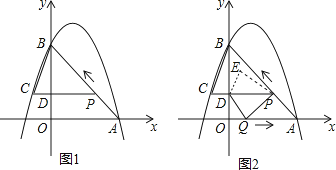
(1)求二次函数y=﹣x2+bx+c的表达式;
(2)连接BC,当t= ![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图2,动点P从A出发时,动点Q同时从O出发,在线段OA上沿O→A的方向以1个单位长度的速度运动.当点P与B重合时,P、Q两点同时停止运动,连接DQ,PQ,将△DPQ沿直线PC折叠得到△DPE.在运动过程中,设△DPE和△OAB重合部分的面积为S,直接写出S与t的函数关系及t的取值范围.
【答案】
(1)
解:把A(3,0),B(0,4)代入y=﹣x2+bx+c中得:
![]() 解得
解得 ![]() ,
,
∴二次函数y=﹣x2+bx+c的表达式为:y=﹣x2+ ![]() x+4
x+4
(2)
解:如图1,
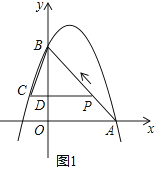
当t= ![]() 时,AP=2t,
时,AP=2t,
∵PC∥x轴,
∴ ![]() ,
,
∴ ![]() ,
,
∴OD= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
当y= ![]() 时,
时, ![]() =﹣x2+
=﹣x2+ ![]() x+4,
x+4,
3x2﹣5x﹣8=0,
x1=﹣1,x2= ![]() ,
,
∴C(﹣1, ![]() ),
),
由 ![]() 得
得 ![]() ,
,
则PD=2,
∴S△BCP= ![]() ×PC×BD=
×PC×BD= ![]() ×3×
×3× ![]() =4
=4
(3)
解:如图3,
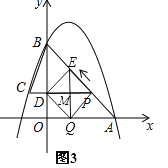
当点E在AB上时,
由(2)得OD=QM=ME= ![]() ,
,
∴EQ= ![]() ,
,
由折叠得:EQ⊥PD,则EQ∥y轴
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
同理得:PD=3﹣ ![]() ,
,
∴当0≤t≤ ![]() 时,S=S△PDQ=
时,S=S△PDQ= ![]() ×PD×MQ=
×PD×MQ= ![]() ×(3﹣
×(3﹣ ![]() )×
)× ![]() ,
,
S=﹣ ![]() t2+
t2+ ![]() t;
t;
当 ![]() <t≤2.5时,
<t≤2.5时,
如图4,
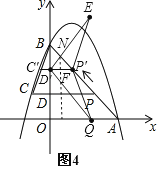
P′D′=3﹣ ![]() ,
,
点Q与点E关于直线P′C′对称,则Q(t,0)、E(t, ![]() ),
),
∵AB的解析式为:y=﹣ ![]() x+4,
x+4,
D′E的解析式为:y= ![]() x+
x+ ![]() t,
t,
则交点N( ![]() ,
, ![]() ),
),
∴S=S△P′D′N= ![]() ×P′D′×FN=
×P′D′×FN= ![]() ×(3﹣
×(3﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() ),
),
∴S= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() .
.
【解析】(1)直接将A、B两点的坐标代入列方程组解出即可;(2)如图1,要想求△BCP的面积,必须求对应的底和高,即PC和BD;先求OD,再求BD,PC是利用点P和点C的横坐标求出,要注意符号;(3)分两种情况讨论:①△DPE完全在△OAB中时,即当0≤t≤ ![]() 时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当
时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当 ![]() <t≤2.5时,如图4所示,△PDN就是重合部分的面积S.本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式,并能利用方程组求出两图象的交点,把方程和函数有机地结合在一起,使函数问题简单化;同时考查了分类讨论的思想,这一思想在二次函数中经常运用,要熟练掌握;本题还与相似结合,利用相似三角形对应边的比来表示线段的长.
<t≤2.5时,如图4所示,△PDN就是重合部分的面积S.本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式,并能利用方程组求出两图象的交点,把方程和函数有机地结合在一起,使函数问题简单化;同时考查了分类讨论的思想,这一思想在二次函数中经常运用,要熟练掌握;本题还与相似结合,利用相似三角形对应边的比来表示线段的长.


科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.
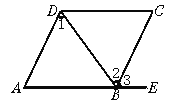
(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.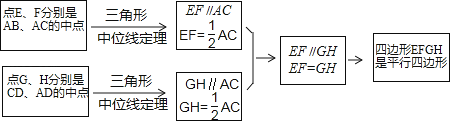
结合小敏的思路作答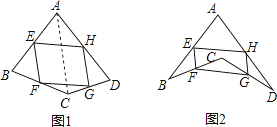
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“爱我汕头,创文同行”的活动,倡议学生利用双休日参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:

(1)抽查的学生劳动时间为1.5小时”的人数为 人,并将条形统计图补充完整.
(2)抽查的学生劳动时间的众数为 小时,中位数为 小时.
(3)已知全校学生人数为1200人,请你估算该校学生参加义务劳动1小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张家界到长沙的距离约为320km,小明开着大货车,小华开着小轿车,都从张家界同时去长沙,已知小轿车的速度是大货车的1.25倍,小华比小明提前1小时到达长沙.试问:大货车和小轿车的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.
(1)若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.
(3)若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com