
【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.

【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)a2+b2+c2=45;
(3)①画图见解析;②2a2+5ab+2b2=(2a+b)(a+2b).
【解析】试题分析:(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.(3)①找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件;②根据所给的规律分解因式即可.
试题解析:
(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,
=112﹣2×38=45;
(3)
①如图所示,
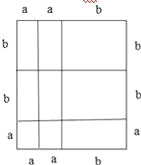
②如上图所示的矩形面积=(2a+b)(a+2b),
它是由2个边长为a的正方形、5个边长分别为a、b的长方形、2个边长为b的小正方形组成,所以面积为2a2+5ab+2b2,则2a2+5ab+2b2=(2a+b)(a+2b),
故答案为:2a2+5ab+2b2=(2a+b)(a+2b).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入![]() 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足 ![]() ,求实数p的值.
,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图形都是由相同的正方形按一定的规律组成,其中:第(1)个图形中的正方形有2个,第(2)个图形中的正方形有5个,第(3)个图形中的正方形有9个,…,按此规律,则第7个图形中的正方形的个数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
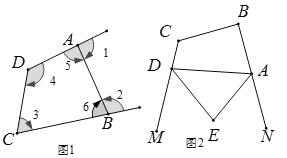
【题目】(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com