
 ,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
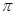 .(1+1+2分)
.(1+1+2分)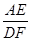 =
=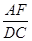 .
. 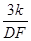 =
=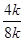
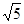 ,BE=5k,BC=10k
,BE=5k,BC=10k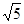 )2
)2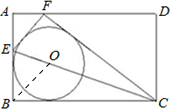
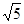 2,
2,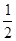 ×BE×BC=
×BE×BC=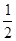 ×BE×r+
×BE×r+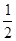 ×BC×r,
×BC×r,

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源:不详 题型:解答题
 为
为 轴正半轴上一点,
轴正半轴上一点, 两点关于
两点关于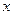 轴对称,过点
轴对称,过点 任作直线交抛物线
任作直线交抛物线 于
于 ,
, 两点
两点
 =∠
=∠ ;
; 的坐标为(0,1),且∠
的坐标为(0,1),且∠ =60º,试求所有满足条件的直线
=60º,试求所有满足条件的直线 的函数解析式.
的函数解析式. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知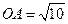 ,
, ,点
,点 的坐标为
的坐标为 .
. 轴上存在一点
轴上存在一点 ,使得
,使得 与
与 相似,请你求出
相似,请你求出 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.25:1 | B.5:1 | C.1:25 | D.1:5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
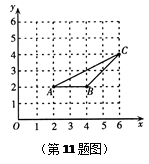
| A.(3,2) | B.(-3,-2)或(3,2) |
C.(2,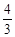 ) ) | D.(2,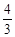 )或(-2,- )或(-2,-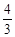 ) ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com