
分析 根据$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{4}{{a}^{2}+{b}^{2}}$,通过变形可以得到a与b的关系,从而可以求得($\frac{b}{a}$)2010-($\frac{a}{b}$)2011的值.
解答 解:∵$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{4}{{a}^{2}+{b}^{2}}$,
∴$\frac{{a}^{2}+{b}^{2}}{{a}^{2}{b}^{2}}=\frac{4}{{a}^{2}+{b}^{2}}$,
∴(a2+b2)2=4a2b2,
∴(a2-b2)2=0,
得a=±b,
当a=b时,原式=12010-12011=1-1=0,
当a=-b时,原式=(-1)2010-(-1)2011
=1-(-1)=2.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
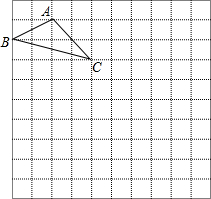 如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向下平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向下平移3格,其中每个格子的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的直径AB⊥弦CD,垂足为点E,点P在优弧CAD上(不包含点C和点D),连PC、PD、CB,tan∠BCD=$\frac{1}{2}$
如图,⊙O的直径AB⊥弦CD,垂足为点E,点P在优弧CAD上(不包含点C和点D),连PC、PD、CB,tan∠BCD=$\frac{1}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com