
 如图,点B、C把$\widehat{AD}$分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是$\frac{π}{8}$.
如图,点B、C把$\widehat{AD}$分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是$\frac{π}{8}$. 分析 根据题意可以求出各个扇形圆心角的度数,然后根据题目中的条件求出阴影部分的面积,本题得以解决.
解答 解:∵点B、C把$\widehat{AD}$分成三等分,ED是⊙O的切线,∠E=45°,
∴∠ODE=90°,∠DOC=45°,
∴∠BOA=∠BOC=∠COD=45°,
∵OD=1,
∴阴影部分的面积是:$\frac{45°×2×π×{1}^{2}}{360}-\frac{1}{2}×(1×\frac{\sqrt{2}}{2})^{2}×2$+$\frac{1}{2}×1×1-\frac{45×π×{1}^{2}}{360}$=$\frac{π}{8}$,
故答案为:$\frac{π}{8}$.
点评 本题考查扇形面积的计算、切线的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
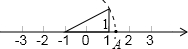 如图所示:数轴上点A所表示的数为a,则a的值是( )
如图所示:数轴上点A所表示的数为a,则a的值是( )| A. | $\sqrt{5}$+1 | B. | -$\sqrt{5}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{-x}$ | B. | y=$\frac{1}{5}$x+1 | C. | y=x2+1 | D. | y=$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com