
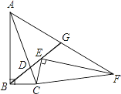
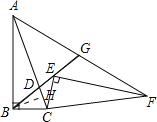
【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为________.
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为________.
【答案】![]()
【解析】
根据旋转的性质可得BC=CE,AC=CF,∠BCE=∠ACF,再根据等腰三角形两底角相等求出∠CBD=∠CAF,从而得到△BCD和△AGD相似,根据相似三角形对应边成比例求出AD=AG,过点B作BH⊥CD于H,根据等腰三角形三线合一的性质可得CD=2CH,再解直角三角形求出CH、AC的长,然后根据AD=AC-CD代入数据进行计算即可得解.
∵△ABC以点C为旋转中心顺时针旋转得到△FEC,
∴BC=CE,AC=CF,∠BCE=∠ACF(为旋转角),
∵∠CBD=![]() (180°-∠BCE),∠CAF=
(180°-∠BCE),∠CAF=![]() (180°-∠ACF),
(180°-∠ACF),
∴∠CBD=∠CAF,
又∵∠BDC=∠ADG,
∴△BCD∽△AGD,
∴![]() =
=![]() ,
,
∵BC=BD,
∴AG=AD,
则CD=2CH,
∵sin∠BAC=![]() ,BC=2,
,BC=2,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得CH=![]() ,AC=6,
,AC=6,
∴CD=2×![]() =
=![]() ,
,
AD=AC-CD=6-![]() =
=![]() ,
,
∴AG=AD=![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了![]() 箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
第 | 第 | 第 | 第 | 第 | |
甲成绩 |
|
|
|
|
|
乙成绩 |
|
|
|
|
|
(1)a=_________
(2)![]()
(3)参照小宇的计算方法,计算乙成绩的方差;
(4)请你从平均数和方差的角度分析,谁将被选中.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,实数
的两实根,实数![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系可能是( )
的大小关系可能是( )
A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
查看答案和解析>>
科目:初中数学 来源: 题型:
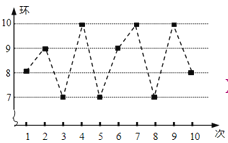
【题目】甲、乙俩射击运动员进行10次射击,甲的成绩是7,7,8,9,8,9,10,9,9,9,乙的成绩如图所示.则甲、乙射击成绩的方差之间关系是![]()
![]() (填“<”,“=”,“>”).
(填“<”,“=”,“>”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌AB,放置在教学楼的顶部(如图所示)。小明在操场上的点D处,用1m高的测角仪CD,从点C测得宣传牌的底部B的仰角为37,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌顶部A仰角为45.已知教学楼高BM=17米,且点A、B、M在同一直线上,求宣传牌AB高度(结果精确到0.1米。参考数据:![]() ,sin37≈0.60,cos37≈0.81,tan37≈0.75).
,sin37≈0.60,cos37≈0.81,tan37≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列两段材料,再解答下列问题:
(一)例题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式
,则原式![]() ,
,
再将“![]() ”换原,得原式
”换原,得原式![]() ;
;
上述解题目用到的是:整体思想,“整体思想”是数学解题中常用的一种思想方法;
(二)常用因式分解的方法有提公因式法和公式法,但有的多项式只用上述一种方法无法分解,例如![]() ,我们细心观察就会发现,前面两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整分解了.
,我们细心观察就会发现,前面两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整分解了.
过程:![]()
![]() ,
,
这种方法叫分组分解法,对于超过三项的多项式往往考虑这种方法.
利用上述数学思想方法解决下列问题:
(1)分解因式:![]()
(2)分解因式:![]()
(3)分解因式:![]() ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com