
【题目】如图,直线y=k1x+b与双曲线![]() 相交于A(1,2),B(m,-1)两点.
相交于A(1,2),B(m,-1)两点.

(1)求直线和双曲线的表达式;
(2)求直线AB与x轴的交点C的坐标及ΔAOB的面积;
(3)观察图像,请直接写出使不等式k1x+b>![]() 成立的x的取值范围.
成立的x的取值范围.
【答案】(1)双曲线的解析式为y=![]() ;直线的解析式为:y=x+1.(2)1.5;(3)x>1或-2<x<0.
;直线的解析式为:y=x+1.(2)1.5;(3)x>1或-2<x<0.
【解析】
(1)先把A点坐标代入![]() 求出k2=2,得到双曲线的解析式为y=
求出k2=2,得到双曲线的解析式为y=![]() ,再把B(m,-1)代入y=
,再把B(m,-1)代入y=![]() 确定B点坐标,然后利用待定系数法确定一次函数的解析式;
确定B点坐标,然后利用待定系数法确定一次函数的解析式;
(2)在直线解析式中令y=0,可求出x的值,从而求出点C的坐标,再根据三角形面积公式求出ΔAOB的面积即可;
(3)观察函数图象得到当x>1或-2<x<0时,一次函数图象都在反比例函数图象上方,即k1x+b>![]() .
.
(1)∵双曲线![]() 经过点A(1,2),
经过点A(1,2),
∴k2=2,
∴双曲线的解析式为y=![]() ;
;
∵点B(m,-1)在双曲线y=![]() 上,
上,
∴m=-2,
∴B点坐标为(-2,-1),
把点A(1,2),B(-2,-1)代入y=k1x+b 得,
 ,解得
,解得![]() ,
,
∴直线的解析式为:y=x+1.
(2)在y=x+1中,令y=0,则x=-1,
∴C(-1,0)
∴S△AOB=![]() =1.5.
=1.5.
(3)由图可知x>1或-2<x<0.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB ,垂足为H,连接AC,过![]() 上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
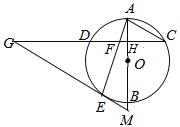
(1)求证:EG是 ⊙O 的切线;
(2)延长AB交GE的延长线于点M ,若tanG=![]() ,AH=2,求 EM 的值.
,AH=2,求 EM 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
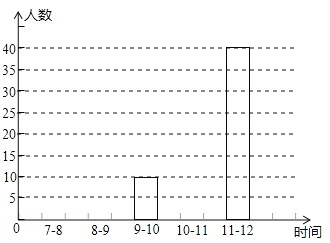

(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过某矩形的两个相对的顶点作平行线,再沿着平行线剪下两个直角三角形,剩余的图形为如图所示的ABCD,AB=4,BC=6,∠ABC=60°,则原来矩形的面积是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
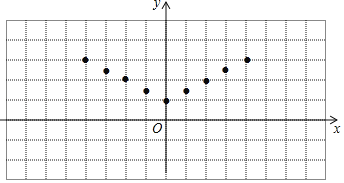
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
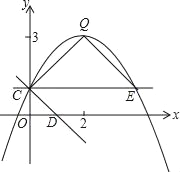
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com