
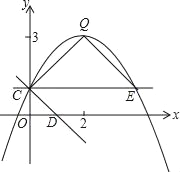
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
【答案】(1)y=﹣x+1;(2)y=![]() x2+2x+1;(3)证明见解析;(4)存在.为
x2+2x+1;(3)证明见解析;(4)存在.为![]() .
.
【解析】试题分析:(1)利用待定系数法求出直线解析式;
(2)利用待定系数法求出抛物线的解析式;
(3)关键是证明△CEQ与△CDO均为等腰直角三角形;
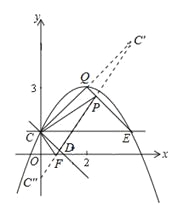
(4)如图所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小.如图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值.
(1)C(0,1),D(1,0)
∴直线CD的解析式为![]() ;
;
(2)设抛物线解析式为y=a(x-2)2+3,
易得y=![]() (x-2)2+3=
(x-2)2+3=![]() x2+2x+1
x2+2x+1
(3)OC=OD,OC⊥OD,∴△OCD为等腰直角三角形,
对称轴x=2与CE交于点M,M(2,1)
易知△QMC与△QME是等腰直角三角形
∴△ CQE也是等腰直角三角形
∴△CEQ∽△CDO
(4)存在。
如图作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称性得:
PC=PC′ CF=C″F
C,C′关于直线QE对称
C′(4,5)
又C″(-1,0) C′C″=![]()
∴△PCF的周长最小值是![]()


科目:初中数学 来源: 题型:
【题目】下图是2019年5月17日至31日某市的空气质量指数趋势图.
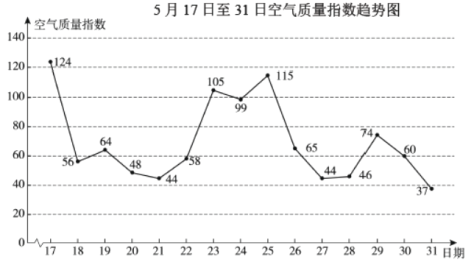
(说明:空气质量指数为0-50、51-100、101-150分别表示空气质量为优、良、轻度污染)
有如下结论:
①在此次统计中,空气质量为优的天数少于轻度污染的天数;
②在此次统计中,空气质量为优良的天数占![]() ;
;
③20,21,22三日的空气质量指数的方差小于26,27,28三日的空气质量指数的方差.
上述结论中,所有正确结论的序号是( )
A.①B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )

A.(S.S.S.) B.(S.A.S.) C.(A.S.A.) D.(A.A.S.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
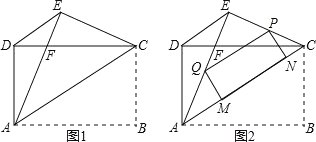
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
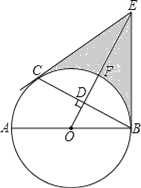
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() 是对角线
是对角线![]() 上的两点,给出下列四个条件:①
上的两点,给出下列四个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中能判定四边形
.其中能判定四边形![]() 是平行四边形的有( )
是平行四边形的有( )
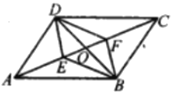
A.①B.①④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现:
任意三个连续偶数的平方和是![]() 的倍数.
的倍数.
验证:
(1)![]() 的结果是
的结果是![]() 的几倍?
的几倍?
(2)设三个连续偶数的中间一个为![]() ,写出它们的平方和,并说明是
,写出它们的平方和,并说明是![]() 的倍数.
的倍数.
延伸:
(3)任意三个连续奇数的平方和,设中间一个为![]() ,被
,被![]() 整除余数是几呢?请写出理由.
整除余数是几呢?请写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y= ![]() 2+b
2+b![]() +c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;
(3)设点P是(1)中的抛物线的一个动点,是否存在满足S△PAB=8的点P?如存在请求出P的坐标;若不存在,请说明理由.


图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为12 ,点B在点A右边,且OA2OB.
(1)写出数轴上点 B 表示的数;
(2)点 M 为数轴上一点,若 AM BM 4 ,求出点 M 表示的数.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com