
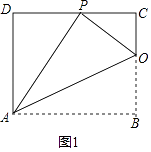
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.且△OCP与△PDA的面积比为1:4
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②求边AB的长;
(2)如图2,连结AP、BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
【答案】
(1)
解:①如图1中,∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴∠DPA+∠DAP=90°,
∵由折叠可得∠APO=∠B=90°,
∴∠DPA+∠CPO=90°,
∴∠DAP=∠CPO,
又∵∠D=∠C,
∴△OCP∽△PDA;
②如图1,∵△OCP与△PDA的面积比为1:4,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴CP= ![]() AD=4,
AD=4,
设OP=x,则CO=8﹣x,
在Rt△PCO中,∠C=90°,
由勾股定理得 x2=(8﹣x)2+42,
解得:x=5,
∴AB=AP=2OP=10,
∴边AB的长为10
(2)
解:结论:线段EF的长度不发生变化.EF=2 ![]() .
.
理由:如图2中,作MQ∥AN,交PB于点Q,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ= ![]() PQ.
PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
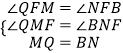 ,
,
∴△MFQ≌△NFB(AAS),
∴QF=FB,
∴QF= ![]() QB,
QB,
∴EF=EQ+QF= ![]() PQ+
PQ+ ![]() QB=
QB= ![]() PB,
PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB= ![]() =4
=4 ![]() ,
,
∴EF= ![]() PB=2
PB=2 ![]() ,
,
∴当点M、N在移动过程中,线段EF的长度不变,它的长度为2 ![]() .
.
【解析】(1)①只要证明∠PAD=∠CPO,由∠D=∠C=90°,即可证出△OCP∽△PDA;②根据△OCP与△PDA的面积比为1:4,得出CP= ![]() AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42 , 求出x,最后根据AB=2OP即可求出边AB的长;(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=
AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42 , 求出x,最后根据AB=2OP即可求出边AB的长;(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ= ![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF= ![]() QB,再求出EF=
QB,再求出EF= ![]() PB,由(1)中的结论求出PB,即可判断.
PB,由(1)中的结论求出PB,即可判断.


 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,当△PMN为等腰三角形时,求此时EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°, ![]() ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度; 
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值; 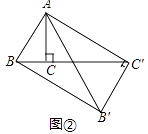
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)计算:|﹣ ![]() |+(π﹣3)0+(
|+(π﹣3)0+( ![]() )﹣1﹣2cos45°
)﹣1﹣2cos45°
(2)若关于x的一元二次方程x2+(k+3)x+k=0的一个根是﹣2,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C. 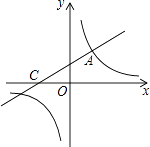
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com