
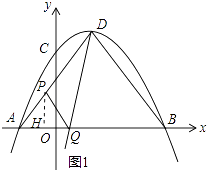
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=�� ![]() x2+bx+c��x�ύ���A����3��0������B��9��0������y�ύ���C������ΪD������AD��DB����PΪ�߶�AD��һ���㣮
x2+bx+c��x�ύ���A����3��0������B��9��0������y�ύ���C������ΪD������AD��DB����PΪ�߶�AD��һ���㣮
��1���������ߵĽ���ʽ��
��2������P��BD��ƽ���ߣ���AB�ڵ�Q������DQ����AQ=m����PDQ�����ΪS����S����m�ĺ�������ʽ���Լ�S�����ֵ��
��3����ͼ2�������߶Գ�����x�ύ���G��EΪOG���е㣬FΪ��C����DG�ԳƵĶԳƵ㣬����P�ֱ���ֱ��EF��DG�Ĵ��ߣ�����ΪM��N������MN������PMNΪ����������ʱ�����ʱEM�ij���
���𰸡�
��1��
�⣺��a=�� ![]() ����������x�ύ���A����3��0������B��9��0����
����������x�ύ���A����3��0������B��9��0����
����Լ��������߽���ʽΪy=�� ![]() ��x+3����x��9��=��
��x+3����x��9��=�� ![]() x2+
x2+ ![]() x+6��
x+6��
�������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+6
x+6
��2��
�⣺��y=�� ![]() x2+
x2+ ![]() x+6=��
x+6=�� ![]() ��x��3��2+8��
��x��3��2+8��
�ඥ��D���꣨3��8����
��AD=DB=10��
���DAB=��DBA��
��PQ��BD��
���PQA=��DBA��
���PAQ=��PQA��
��PA=PQ��
���PAQ����������
��PH��AQ��H����AH=HQ= ![]() ����ͼ1�У���
����ͼ1�У���
��tan��DAB= ![]() =
= ![]() ��
��
��PH= ![]() m��
m��
��S=S��ADQ��S��APQ= ![]() m8��
m8�� ![]() m
m ![]() m=��
m=�� ![]() m2+4m=��
m2+4m=�� ![]() ��m��6��2+12��
��m��6��2+12��
�൱m=6ʱ��S���ֵ=12
��3��
�⣺��E�� ![]() ��0����F��6��6����
��0����F��6��6����
��ֱ��EF����ʽΪy= ![]() x��2��ֱ��AD����ʽΪy=
x��2��ֱ��AD����ʽΪy= ![]() x+4��
x+4��
��EF��AD����EL��AD��L������ͼ2�У�
��AE= ![]() ��sin��DAB=
��sin��DAB= ![]() ��
��
��LE= ![]() ��
�� ![]() =
= ![]() =PM��
=PM��
��PM=PN= ![]() ʱ��
ʱ��
��xP=3�� ![]() =��
=�� ![]() ��yP=��
��yP=�� ![]() ��
�� ![]() +4=
+4= ![]() ��
��
��P���� ![]() ��
�� ![]() ����
����
��ֱ��PM����ʽΪy=�� ![]() x+
x+ ![]() ��
��
�� 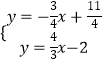 �����
����� 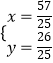 ��
��
���M�� ![]() ��
�� ![]() ��
��
��EM= ![]() =
= ![]() ��
��
��NP=NMʱ����ֱ��EF��Գ��ύ�ڵ�K��K��3��2����
��ʱ��N��PM�Ĵ�ֱƽ�����ϣ�DN=NK��
��N��3��5����P�� ![]() ��5����
��5����
��ֱ��PM�Ľ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
�� 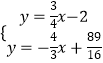 ���
��� 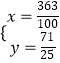 ��
��
��M�� ![]() ��
�� ![]() ����
����
��EM= ![]() =
= ![]() ��
��
��PM=MNʱ��cos��MPN= ![]() =
= ![]() ��
��
��PN= ![]() ���ɴ˿ɵ�P����
���ɴ˿ɵ�P���� ![]() ��
�� ![]() ����
����
��ֱ��PM����ʽΪy=�� ![]() x��
x�� ![]() ��
��
�� 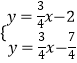 ���
��� 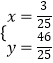 ��
��
��M�� ![]() ����
���� ![]() ����
����
��EM= ![]() =
= ![]() ��
��
����������EM= ![]() ��
�� ![]() ��
�� ![]() ��
��
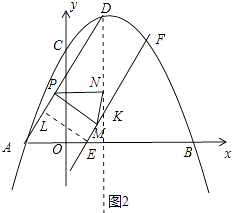
����������1�����Լ��������߽���ʽΪy=�� ![]() ��x+3����x��9����չ�����ɣ���2����PH��AQ��H����AH=HQ=
��x+3����x��9����չ�����ɣ���2����PH��AQ��H����AH=HQ= ![]() ����ͼ1�У�������S=S��ADQ��S��APQ�������κ��������ö��κ��������ʼ��ɽ�����⣮��3���������������ۢ�PM=PN����NP=NM����MN=MP���ֱ����ֱ��PM�Ľ���ʽ�����÷����������M���꼴�ɽ�����⣮
����ͼ1�У�������S=S��ADQ��S��APQ�������κ��������ö��κ��������ʼ��ɽ�����⣮��3���������������ۢ�PM=PN����NP=NM����MN=MP���ֱ����ֱ��PM�Ľ���ʽ�����÷����������M���꼴�ɽ�����⣮
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������˽������ѵ�������˷ֱ����12�Σ���ͼ�ֱ�ͳ�������˵�����ɼ�����֪������ɼ��ķ���S��2= ![]() ��ƽ���ɼ�
��ƽ���ɼ� ![]() =8.5��
=8.5�� 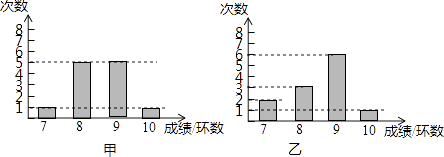
��1������ͼ����Ϣ������������ɼ�������9���ĸ����Ƕ��٣�
��2�����������ƽ���ɼ��ķ�����ݴ˱Ƚϼ��ҵ������ˮƽ����
S2= ![]() [��x1��
[��x1�� ![]() ��2+��x2��
��2+��x2�� ![]() ��2����xn��
��2����xn�� ![]() ��2]��
��2]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+3��x�ᡢy��ֱ��ཻ�ڵ�B��C������B��C�����������y=ax2+bx+c��x�����һ������ΪA������ΪP���ҶԳ���Ϊֱ��x=2��
��1����������ߵĽ���ʽ��
��2������PB��PC�����PBC�������
��3������AC����x�����Ƿ����һ��Q��ʹ���Ե�P��B��QΪ��������������ABC���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD������EAF=45�㣬AE��BC�ڵ�E��AF��CD�ڵ�F������EF������A��AH��EF������ΪH��
��1����ͼ2������ADF�Ƶ�A˳ʱ����ת90��õ���ABG��
����֤����AGE�ա�AFE��
����BE=2��DF=3����AH�ij���
��2����ͼ3������BD��AE�ڵ�M����AF�ڵ�N����̽�������룺�߶�BM��MN��ND֮����ʲô������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ4��������ABCD�ڽ��ڵ�O����E�� ![]() �ϵ�һ���㣨����A��B�غϣ�����F��
�ϵ�һ���㣨����A��B�غϣ�����F�� ![]() �ϵ�һ�㣬����OE��OF���ֱ���AB��BC���ڵ�G��H���ҡ�EOF=90�㣬�����½��ۣ� ��
�ϵ�һ�㣬����OE��OF���ֱ���AB��BC���ڵ�G��H���ҡ�EOF=90�㣬�����½��ۣ� �� ![]() =
= ![]() ��
��
�ڡ�OGH�ǵ��������Σ�
���ı���OGBH��������ŵ�Eλ�õı仯���仯��
�ܡ�GBH�ܳ�����СֵΪ4+ ![]() ��
��
������ȷ������������Ϊ��ȷ���۵���Ŷ����ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC��AB=AC����ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E����F��AC���ӳ����ϣ��ҡ�CBF= ![]() ��CAB��
��CAB�� 
��1����֤��ֱ��BF�ǡ�O�����ߣ�
��2����AB=5��sin��CBF= ![]() ����BC��BF�ij���
����BC��BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���C=90�㣬AC=8cm��BC=6cm���Ե�CΪԲ��5cmΪ�뾶��Բ��ֱ��AB��λ�ù�ϵ�ǣ� ��
A.�ཻ
B.����
C.����
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD��һ����AD=8��������ABCD�۵���ʹ�ö���B����CD���ϵ�P�㴦���ҡ�OCP���PDA�������Ϊ1��4
��1����ͼ1����֪�ۺ����BC���ڵ�O������AP��OP��OA��
����֤����OCP�ס�PDA��
�����AB�ij���
��2����ͼ2������AP��BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com