
【题目】如图,直线y=﹣x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
(1)求该抛物线的解析式;
(2)连接PB、PC,求△PBC的面积;
(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵直线y=﹣x+3与x轴相交于点B,
∴当y=0时,x=3,
∴点B的坐标为(3,0),
∵y=﹣x+3过点C,易知C(0,3),
∴c=3.
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,
根据抛物线的对称性,
∴点A的坐标为(1,0).
又∵抛物线y=ax2+bx+c过点A(1,0),B(3,0),
∴ ![]()
解得: ![]()
∴该抛物线的解析式为:y=x2﹣4x+3
(2)
解:如图1,∵y=x2﹣4x+3=(x﹣2)2﹣1,
又∵B(3,0),C(0,3),
∴PC= ![]() =
= ![]() =2
=2 ![]() ,PB=
,PB= ![]() =
= ![]() ,
,
∴BC= ![]() =
= ![]() =3
=3 ![]() ,
,
又∵PB2+BC2=2+18=20,PC2=20,
∴PB2+BC2=PC2,
∴△PBC是直角三角形,∠PBC=90°,
∴S△PBC= ![]() PBBC=
PBBC= ![]() ×
× ![]() ×3
×3 ![]() =3
=3
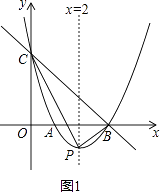
(3)
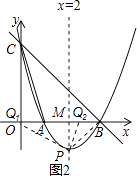
解:如图2,由y=x2﹣4x+3=(x﹣2)2﹣1,得P(2,﹣1),
设抛物线的对称轴交x轴于点M,
∵在Rt△PBM中,PM=MB=1,
∴∠PBM=45°,PB= ![]() .
.
由点B(3,0),C(0,3)易得OB=OC=3,在等腰直角三角形OBC中,∠ABC=45°,
由勾股定理,得BC=3 ![]() .
.
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当 ![]() =
= ![]() ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即 ![]() =
= ![]() ,
,
解得:BQ=3,
又∵BO=3,
∴点Q与点O重合,
∴Q1的坐标是(0,0).
②当 ![]() =
= ![]() ,∠QBP=∠ABC=45°时,△QBP∽△ABC.
,∠QBP=∠ABC=45°时,△QBP∽△ABC.
即 ![]() =
= ![]() ,
,
解得:QB= ![]() .
.
∵OB=3,
∴OQ=OB﹣QB=3﹣ ![]() ,
,
∴Q2的坐标是( ![]() ,0).
,0).
③当Q在B点右侧,
则∠PBQ=180°﹣45°=135°,∠BAC<135°,
故∠PBQ≠∠BAC.
则点Q不可能在B点右侧的x轴上,
综上所述,在x轴上存在两点Q1(0,0),Q2( ![]() ,0),
,0),
能使得以点P,B,Q为顶点的三角形与△ABC相似.
【解析】本题主要考查待定系数法、方程、函数及三角形相似等知识,也考查了综合运用数学知识、分析问题、解决问题的能力以及数形结合、分类讨论的思想,正确运用分类讨论是解题关键.(1)根据二次函数的对称性,已知对称轴的解析式以及B点的坐标,即可求出A的坐标,利用抛物线过A、B、C三点,可用待定系数法来求函数的解析式(2)首先利用各点坐标得出得出△PBC是直角三角形,进而得出答案;(3)本题要先根据抛物线的解析式求出顶点P的坐标,然后求出BP的长,进而分情况进行讨论:①当 ![]() =
= ![]() ,∠PBQ=∠ABC=45°时,根据A、B的坐标可求出AB的长,根据B、C的坐标可求出BC的长,已经求出了PB的长度,那么可根据比例关系式得出BQ的长,即可得出Q的坐标.②当
,∠PBQ=∠ABC=45°时,根据A、B的坐标可求出AB的长,根据B、C的坐标可求出BC的长,已经求出了PB的长度,那么可根据比例关系式得出BQ的长,即可得出Q的坐标.②当 ![]() =
= ![]() ,∠QBP=∠ABC=45°时,可参照①的方法求出Q的坐标.③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
,∠QBP=∠ABC=45°时,可参照①的方法求出Q的坐标.③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 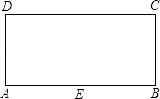
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的 ![]() .
. 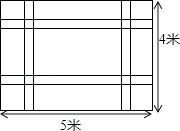
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.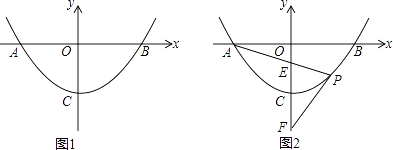
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( ) 
A.(4,3)
B.(5, ![]() )
)
C.(4, ![]() )
)
D.(5,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上. 
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 ![]() x+b<
x+b< ![]() 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,当△PMN为等腰三角形时,求此时EM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com