
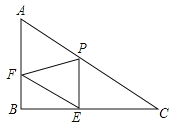
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
【答案】(1)![]() (0<x<20);(2)当x=10或x=16,存在点P使△PEF是Rt△.
(0<x<20);(2)当x=10或x=16,存在点P使△PEF是Rt△.
【解析】
试题分析:(1)在Rt△ABC中,根据三角函数可求y与x的函数关系式;
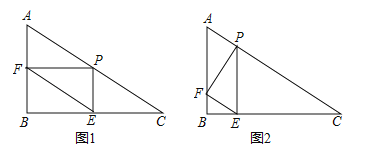
(2)分三种情况:①如图1,当∠FPE=90°时,②如图2,当∠PFE=90°时,③当∠PEF=90°时,进行讨论可求x的值.
试题解析:(1)在Rt△ABC中,∠B=90°,AC=20,AB=10,∴sinC=![]() ,∵PE⊥BC于点E,∴sinC=
,∵PE⊥BC于点E,∴sinC=![]() =
=![]() ,∵PC=x,PE=y,∴
,∵PC=x,PE=y,∴![]() (0<x<20);
(0<x<20);
(2)存在点P使△PEF是Rt△,①如图1,当∠FPE=90°时,四边形PEBF是矩形,BF=PE=![]() x,四边形APEF是平行四边形,PE=AF=
x,四边形APEF是平行四边形,PE=AF=![]() x,∵BF+AF=AB=10,∴x=10;
x,∵BF+AF=AB=10,∴x=10;
②如图2,当∠PFE=90°时,Rt△APF∽Rt△ABC,∠ARP=∠C=30°,AF=40﹣2x,平行四边形AFEP中,AF=PE,即:40﹣2x=![]() x,解得x=16;
x,解得x=16;
③当∠PEF=90°时,此时不存在符合条件的Rt△PEF.
综上所述,当x=10或x=16,存在点P使△PEF是Rt△.


科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形错误的是 ( )
A.y-x = x-yB.-a-b=-(a+b)
C.(y-x)2=(x-y)2D.(a-b)3=-(b-a)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数y=﹣2(x﹣2)2+1图象的叙述,其中错误的是( )
A. 开口向下 B. 对称轴是直线x=2
C. 此函数有最小值是1 D. 当x>2时,函数y随x增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将△ABC的三个顶点的纵坐标保持不变,横坐标分别乘以-1,依次连接新的这些点,则所得三角形与原三角形的位置关系是( )
A. 原三角形向x轴的负方向平移一个单位即为所得三角形
B. 关于原点对称
C. 关于x轴对称
D. 关于y轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com