
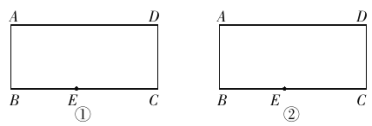
【题目】在图①②中,点E在矩形ABCD的边BC上,且BE=AB,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法]
(1)在图①中,画∠BAD的平分线;
(2)在图②中,画∠BCD的平分线.
【答案】(1)见解析;(2)见解析
【解析】
(1)连接AE,等边对等角可得∠BAE=∠BEA=45![]() ,再根据平行线的性质即可得到AE是∠BAD的平分线;
,再根据平行线的性质即可得到AE是∠BAD的平分线;
(2)连接矩形ABCD的对角线,交于点O,可得AO=CO,再连接EO并延长,交BC于P,根据△APO≌△CEO,可得AP=CE,得到四边形AECP为平行四边形,得到∠ECP=∠BEA=45![]() ,即可得到CP是∠BCD的平分线.
,即可得到CP是∠BCD的平分线.
(1)如图所示,AE即为所求;
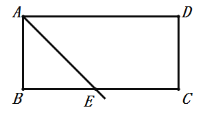
∵点E在矩形ABCD的边BC上,且BE=AB,
∴∠B=90![]() ,∠BAE=∠BEA=45
,∠BAE=∠BEA=45![]() ,
,
∵AD∥BC,
∴∠DAE=∠BEA=45![]() ,
,
∴∠DAE=∠BAE,
∴AE是∠BAD的平分线;
(2)如图所示,CP即为所求;
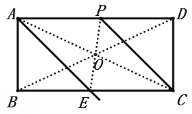
∵四边形ABCD是矩形,
∴AP∥EC,
∴∠PAO=∠ECO,
点O是矩形ABCD对角线的交点,
∴AO=CO,
∵∠POA=∠EOC,
∴△APO≌△CEO,
∴AP=CE,
又∵AP∥EC,
∴四边形AECP为平行四边形,
∴AE∥PC,
∴∠ECP=∠BEA=45![]() ,
,
∴CP是∠BCD的平分线.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】春临大地,学校决定给长12米,宽9米的一块长方形展示区进行种植改造现将其划分成如图两个区域:区域Ⅰ矩形ABCD部分和区域Ⅱ四周环形部分,其中区域Ⅰ用甲、乙、丙三种花卉种植,且EF平分BD,G,H分别为AB,CD中点.
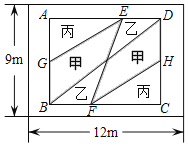
(1)若区域Ⅰ的面积为Sm2,种植均价为180元/m2,区域Ⅱ的草坪均价为40元/m2,且两区域的总价为16500元,求S的值.
(2)若AB:BC=4:5,区域Ⅱ左右两侧草坪环宽相等,均为上、下草坪环宽的2倍
①求AB,BC的长;
②若甲、丙单价和为360元/m2,乙、丙单价比为13:12,三种花卉单价均为20的整数倍.当矩形ABCD中花卉的种植总价为14520元时,求种植乙花卉的总价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点E,在弦BC上取一点F,使AF=AE,连接AF并延长交⊙O于点D.
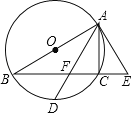
(1)求证:∠B=∠CAD;
(2)若CE=2,∠B=30°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=6.
,BC=6.
(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点
的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需
证明).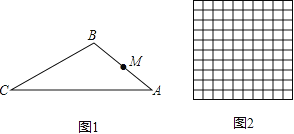
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A,D两点,交AB于点E,交AC于点F
(1)求证:BC是⊙O的切线;
(2)若⊙O半径是2cm,F是弧AD的中点,求阴影部分的面积(结果保留π和根号)
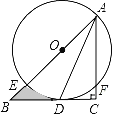
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,连接BD.
(1)求证:∠A=∠CBD.
(2)若AB=10,AD=6,M为线段BC上一点,请写出一个BM的值,使得直线DM与⊙O相切,并说明理由.
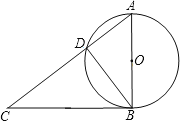
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com