
【题目】某中学为促进阳光体育运动发展,计划购进足球、排球充实体育器材,若购买足球30个、排球20个,共需资金2600元,若购买足球40个、排球30个,共需资金3600元.
(1)求足球、排球的价格分别是多少元?
(2)若该校计划购进这两种球的总数是60个,学校至多能够提供资金2800元,求最多能购买足球多少个?
【答案】(1)足球的单价为60元,排球的单价为40元;(2)最多能购买20个足球.
【解析】
(1)设足球的单价为x元/个,篮球的单价为y元/个,根据购买足球30个、排球20个,共需资金2600元,若购买足球40个、排球30个,共需资金3600元即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买足球x个,则购买篮球(50-x)个,根据总价=单价×数量,结合总资金不超过2800元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其最大值即可.
解:(1)设足球、排球的单价分别为![]() 元,
元,![]() 元,依题意得:
元,依题意得:
![]()
解得![]()
即足球的单价为60元,排球的单价为40元.
(2)设购买足球![]() 个,则购买排球为
个,则购买排球为![]() 个,依题得:
个,依题得:
![]()
解得:![]()
即最多能购买20个足球.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)当AB=4![]() 且
且![]() =
=![]() 时,求劣弧
时,求劣弧![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想知道一堵墙上点A的高度(AO⊥OD),但又没有直接测量的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
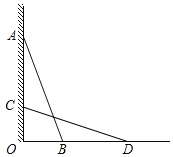
第一步:找一根长度大于OA的直杆,使直杆靠在墙上,且顶端与点A重合,记下直杆与地面的夹角∠ABO;
第二步:使直杆顶端竖直缓慢下滑,直到∠ =∠ .标记此时直杆的底端点D;
第三步:测量 的长度,即为点A的高度.
说明理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(﹣5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
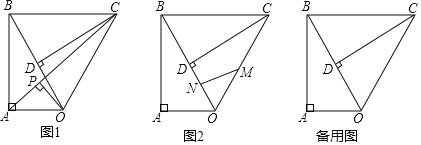
【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC.
(1)填空:∠OBC= °;
(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
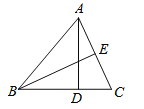
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于点F,BF=AC, ∠ABE=22°,则∠CAD的度数是________°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com