
【题目】小明想知道一堵墙上点A的高度(AO⊥OD),但又没有直接测量的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
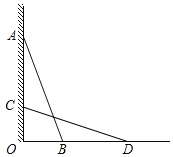
第一步:找一根长度大于OA的直杆,使直杆靠在墙上,且顶端与点A重合,记下直杆与地面的夹角∠ABO;
第二步:使直杆顶端竖直缓慢下滑,直到∠ =∠ .标记此时直杆的底端点D;
第三步:测量 的长度,即为点A的高度.
说明理由:
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
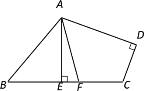
【题目】如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作体验
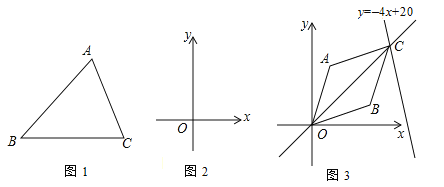
(1)如图1,已知△ABC,请画出△ABC的中线AD,并判断△ABD与△ACD的面积大小关系.
(2)如图2,在平面直角坐标系中,△ABC的边BC在x轴上,已知点A(2,4),B(–1,0),C(3,0),试确定过点A的一条直线l,平分△ABC的面积,请写出直线l的表达式.
综合运用
(3)如图3,在平面直角坐标系中,如果A(1,4),B(3,2),那么在直线y=–4x+20上是否存在一点C,使直线OC恰好平分四边形OACB的面积?若存在,请计算点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
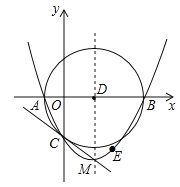
【题目】如图,抛物线y=![]() (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图书馆与学校相距600m,明明从学校出发步行去图书馆,亮亮从图书馆骑车去学校两人同时出发,匀速相向而行,他们与学校的距离S(m)与时间t(s)的图象如图所示:
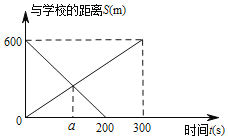
根据图象回答:
(1)明明步行的速度为 m/s;亮亮骑车的速度为 m/s.
(2)分別写出明明、亮亮与学校的距离S1、S2与时间t的关系式.
(3)通过计算求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:若要比较![]() 与
与![]() 的大小.我们可以利用不等式的性质来说明:
的大小.我们可以利用不等式的性质来说明:
例加:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
像上述比较两个代数式大小的方法叫做作差法.
如:某同学需要比较![]() 与
与![]() 的大小,做法为
的大小,做法为![]() ,则
,则![]() .试解答下列问题:
.试解答下列问题:
(1) 比较大小:![]()
![]()
(2) 若![]() ,试用作差法比较
,试用作差法比较![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(3)若某三角形的底和高均为![]() ,某长方形的长宽为
,某长方形的长宽为![]() 和
和![]() ,试比较这两个图形的面积大小,并说明理由;(其中
,试比较这两个图形的面积大小,并说明理由;(其中![]() )
)
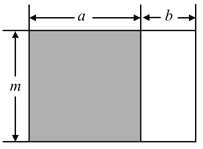
(4)“无字证明”是数学中非常重要的一种解决方法.课本在证明![]() 时,运用了如图中的图形面积来证明.某同学提出运用图形的几何意义的方法不仅可以解决等式的证明,也可以解决不等式的相关证明.如对(2)问中的
时,运用了如图中的图形面积来证明.某同学提出运用图形的几何意义的方法不仅可以解决等式的证明,也可以解决不等式的相关证明.如对(2)问中的![]() 的大小关系的证明,当
的大小关系的证明,当![]() 时,若使用图形的几何意义可以更为直观解决,请你画出符合题意的图形,并简要说明.
时,若使用图形的几何意义可以更为直观解决,请你画出符合题意的图形,并简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为促进阳光体育运动发展,计划购进足球、排球充实体育器材,若购买足球30个、排球20个,共需资金2600元,若购买足球40个、排球30个,共需资金3600元.
(1)求足球、排球的价格分别是多少元?
(2)若该校计划购进这两种球的总数是60个,学校至多能够提供资金2800元,求最多能购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com