
【题目】如图,抛物线y=![]() (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
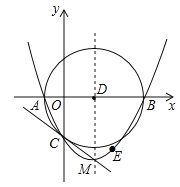
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】①根据抛物线的解析式得出抛物线与x轴的交点A、B坐标,由抛物线的对称性即可判定;②求得⊙D的直径AB的长,得出其半径,由圆的面积公式即可判定;③过点C作CE∥AB,交抛物线于E,如果CE=AD,则根据一组等边平行且相等的四边形是平行四边形即可判定;④求得直线CM、直线CD的解析式通过它们的斜率进行判定.
∵在y=![]() (x+2)(x﹣8)中,当y=0时,x=﹣2或x=8,
(x+2)(x﹣8)中,当y=0时,x=﹣2或x=8,
∴点A(﹣2,0)、B(8,0),
∴抛物线的对称轴为x=![]() =3,故①正确;
=3,故①正确;
∵⊙D的直径为8﹣(﹣2)=10,即半径为5,
∴⊙D的面积为25π,故②错误;
在y=![]() (x+2)(x﹣8)=
(x+2)(x﹣8)=![]() x2﹣
x2﹣![]() x﹣4中,当x=0时y=﹣4,
x﹣4中,当x=0时y=﹣4,
∴点C(0,﹣4),
当y=﹣4时,![]() x2﹣
x2﹣![]() x﹣4=﹣4,
x﹣4=﹣4,
解得:x1=0、x2=6,
所以点E(6,﹣4),
则CE=6,
∵AD=3﹣(﹣2)=5,
∴AD≠CE,
∴四边形ACED不是平行四边形,故③错误;
∵y=![]() x2﹣
x2﹣![]() x﹣4=
x﹣4=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
∴点M(3,﹣![]() ),
),
∴DM=![]() ,
,
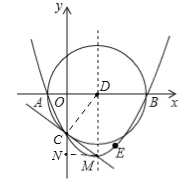
如图,连接CD,过点M作MN⊥y轴于点N,则有N(0,﹣![]() ),MN=3,
),MN=3,
∵C(0,-4),∴CN=![]() ,∴CM2=CN2+MN2=
,∴CM2=CN2+MN2=![]() ,
,
在Rt△ODC中,∠COD=90°,∴CD2=OC2+OD2=25,∴CM2+CD2=![]() ,
,
∵DM2=![]() ,
,
∴CM2+CD2=DM2,
∴∠DCM=90°,即DC⊥CM,
∵CD是半径,
∴直线CM与⊙D相切,故④正确,
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了![]() 元”.
元”.

表1
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 |
|
|
买调料 |
|
|
总计 |
|
|
(1)为了解释“剩余金额总计”与“我手里有![]() 元”无关,按要求填写表2中的空格.
元”无关,按要求填写表2中的空格.
表2
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 | 元 | 元 |
买调料 | 元 |
|
总计 |
|
|
表3
花去 | 剩余 | |
买物品1 |
|
|
买物品2 |
|
|
买物品3 |
|
|
买物品4 |
|
|
总计 |
|
|
(2)如表3中,直接写出以下各代数式的值:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(3)如表3中,![]() 都是正整数,则
都是正整数,则![]() 的最大值等于 ;最小值等于 .由此可以知道“为什么多出了
的最大值等于 ;最小值等于 .由此可以知道“为什么多出了![]() 元”只是一个诡辩而已.
元”只是一个诡辩而已.
(4)我们将“花去”记为“![]() ”,“剩余”记为“
”,“剩余”记为“![]() ”,请在表4中将表1数据重新成号.
”,请在表4中将表1数据重新成号.
花去 | 剩余 | |
买牛肉 | 元 | 元 |
买猪脚 | 元 | 元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 元 |
总计 | 元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④![]() .
.
![]()
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想知道一堵墙上点A的高度(AO⊥OD),但又没有直接测量的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
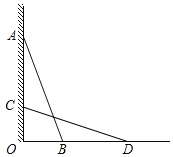
第一步:找一根长度大于OA的直杆,使直杆靠在墙上,且顶端与点A重合,记下直杆与地面的夹角∠ABO;
第二步:使直杆顶端竖直缓慢下滑,直到∠ =∠ .标记此时直杆的底端点D;
第三步:测量 的长度,即为点A的高度.
说明理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
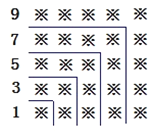
【题目】数学课堂上,老师提出问题:如图,如何在该图形中数出黑色正方形的个数,以下是两位同学的做法:
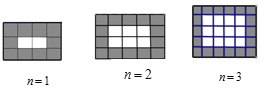
(1)甲同学的做法为:
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
……则在第![]() 个图形中,黑色正方形的个数共有 (无需化简)
个图形中,黑色正方形的个数共有 (无需化简)
(2)乙同学的做法为:
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
……则在第![]() 个图形中,黑色正方形的个数共有 (无需化简)
个图形中,黑色正方形的个数共有 (无需化简)
(3)数学老师及时肯定了两位同学的做法,从而可以得到等式
(4)请利用学习过的知识验证(3)问中的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com