
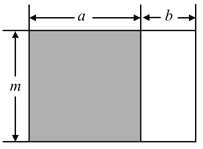
����Ŀ����ѧ�����ϣ���ʦ������⣺��ͼ������ڸ�ͼ����������ɫ�����εĸ�������������λͬѧ��������
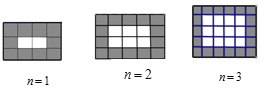
��1����ͬѧ������Ϊ��
��![]() ʱ����ɫ�����εĸ�������
ʱ����ɫ�����εĸ�������![]()
��![]() ʱ����ɫ�����εĸ�������
ʱ����ɫ�����εĸ�������![]()
��![]() ʱ����ɫ�����εĸ�������
ʱ����ɫ�����εĸ�������![]()
�������ڵ�![]() ��ͼ���У���ɫ�����εĸ������� �����軯��
��ͼ���У���ɫ�����εĸ������� �����軯��
��2����ͬѧ������Ϊ��
��![]() ʱ����ɫ�����εĸ�������
ʱ����ɫ�����εĸ�������![]()
��![]() ʱ����ɫ�����εĸ�������
ʱ����ɫ�����εĸ�������![]()
��![]() ʱ����ɫ�����εĸ�������
ʱ����ɫ�����εĸ�������![]()
�������ڵ�![]() ��ͼ���У���ɫ�����εĸ������� �����軯��
��ͼ���У���ɫ�����εĸ������� �����軯��
��3����ѧ��ʦ��ʱ�϶�����λͬѧ���������Ӷ����Եõ���ʽ
��4��������ѧϰ����֪ʶ��֤��3�����еĵ�ʽ��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4����������
����4����������
��������
��1������������ʽ�ܽ���ɼ��ɣ�
��2������������ʽ�ܽ���ɼ��ɣ�
��3�����������㷨����ȷ�ɵõ�ʽ��
��4��������ʽ������㷨���![]() ���л�������֤.
���л�������֤.
�⣺��1����������ʽ��֪���ڵ�![]() ��ͼ���У���ɫ�����εĸ���Ϊ��
��ͼ���У���ɫ�����εĸ���Ϊ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����������ʽ��֪���ڵ�![]() ��ͼ���У���ɫ�����εĸ���Ϊ��
��ͼ���У���ɫ�����εĸ���Ϊ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3����ѧ��ʦ��ʱ�϶�����λͬѧ���������Ӷ����Եõ���ʽ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��4����![]() ��
��
��õ�ʽ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��DC��AD��BC��E��F��DB��������BF��DE������AEB��120�㣬��ADB��30�������BCF�� ��������

A. 150�� B. 40�� C. 80�� D. 90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ����˶����ϣ�ijѧУ�̹����ѧ������ж���Ͷ��������ÿ���������ѡ�ֲμӣ�ÿ��ѡ��Ͷ��ʮ�Σ�Ͷ�м�1�֣����м���֣�3������(��3��)��Ϊ�ϸ����ɼ����Ƴ�����ͳ��ͼ���£�
Ͷ���ɼ�����ͳ��ͼ
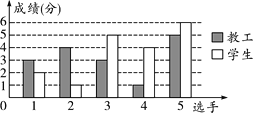
(1)�����������ͳ��ͼ�е�������д����
��� | ƽ���� | ��λ�� | ���� | �ϸ��� |
�̹��� | ________ | 3 | ________ | 80% |
ѧ���� | 3.6 | ________ | 3.44 | 60% |
(2)���С����Ϊ�̹���ijɼ�����ѧ���飬����Ϊ����������ʲô��С����Ϊѧ����ɼ����ڽ̹��飬������������ʲô��
(3)������һ��������ʦͶ����������ʦ�ɼ�ƽ��������ѧ����ɼ�����λ����������������ʦ����m�֣���m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() ��x+2����x��8����x�ύ��A��B���㣬��y�ύ�ڵ�C������ΪM����ABΪֱ������D�����н��ۣ��������ߵĶԳ�����ֱ��x=3���ڡ�D�����Ϊ16�У����������ϴ��ڵ�E��ʹ�ı���ACEDΪƽ���ı��Σ���ֱ��CM���D���У�������ȷ���۵ĸ����ǣ�������
��x+2����x��8����x�ύ��A��B���㣬��y�ύ�ڵ�C������ΪM����ABΪֱ������D�����н��ۣ��������ߵĶԳ�����ֱ��x=3���ڡ�D�����Ϊ16�У����������ϴ��ڵ�E��ʹ�ı���ACEDΪƽ���ı��Σ���ֱ��CM���D���У�������ȷ���۵ĸ����ǣ�������
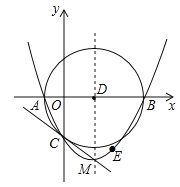
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AB=4��BC=2������ABC�Ƶ�B˳ʱ�뷽����ת����A��BC����λ�ã���ʱ��A��ǡ����CB���ӳ����ϣ���ͼ����Ӱ���ֵ����Ϊ_____����������У���
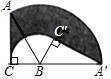
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ���Ҫ�Ƚ�![]() ��
��![]() �Ĵ�С�����ǿ������ò���ʽ��������˵����
�Ĵ�С�����ǿ������ò���ʽ��������˵����
���ӣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��
��
�������Ƚ���������ʽ��С�ķ������������
�磺ijͬѧ��Ҫ�Ƚ�![]() ��
��![]() �Ĵ�С������Ϊ
�Ĵ�С������Ϊ![]() ����
����![]() ���Խ���������⣺
���Խ���������⣺
��1�� �Ƚϴ�С��![]()
![]()
��2�� ��![]() ����������Ƚ�
����������Ƚ�![]() ��
��![]() �Ĵ�С��ϵ����˵�����ɣ�
�Ĵ�С��ϵ����˵�����ɣ�
��3����ij�����εĵ߾�Ϊ![]() ��ij�����εij���Ϊ
��ij�����εij���Ϊ![]() ��
��![]() ���ԱȽ�������ͼ�ε������С����˵�����ɣ�(����
���ԱȽ�������ͼ�ε������С����˵�����ɣ�(����![]() )
)
��4��������֤��������ѧ�зdz���Ҫ��һ�ֽ���������α���֤��![]() ʱ����������ͼ�е�ͼ�������֤����ijͬѧ�������ͼ�εļ�������ķ����������Խ����ʽ��֤����Ҳ���Խ������ʽ�����֤������ԣ�2�����е�
ʱ����������ͼ�е�ͼ�������֤����ijͬѧ�������ͼ�εļ�������ķ����������Խ����ʽ��֤����Ҳ���Խ������ʽ�����֤������ԣ�2�����е�![]() �Ĵ�С��ϵ��֤������
�Ĵ�С��ϵ��֤������![]() ʱ����ʹ��ͼ�εļ���������Ը�Ϊֱ�۽�������㻭�����������ͼ�Σ�����Ҫ˵����
ʱ����ʹ��ͼ�εļ���������Ը�Ϊֱ�۽�������㻭�����������ͼ�Σ�����Ҫ˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ķ�������ϣ����б��A��B��C��3��С��������ǿյأ�����6��С��������Dz�ƺ����������С���������ȫ��ͬ��

��1��һֻ���ɷ��е������������ͼ�еķ�������ϣ���С�����ڲ�ƺ�ϵĸ����Ƕ��٣�
��2���ִ�3��С����յ�������ѡȡ2����ֲ��ƺ����պ�ѡȡA��B��2��С����յ���ֲ��ƺ�ĸ����Ƕ��٣�������ͼ���б�����⣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
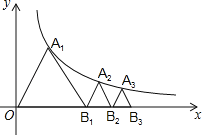
����Ŀ����ͼ����֪�ȱ���OA1B1������A1��˫����y=![]() ��x��0���ϣ���B1������Ϊ��2��0������B1��B1A2��OA1��˫�����ڵ�A2����A2��A2B2��A1B1��x���ڵ�B2���õ��ڶ����ȱ���B1A2B2����B2��B2A3��B1A2��˫�����ڵ�A3����A3��A3B3��A2B2��x���ڵ�B3���õ��������ȱ���B2A3B3���Դ����ƣ��������B6������Ϊ_____��
��x��0���ϣ���B1������Ϊ��2��0������B1��B1A2��OA1��˫�����ڵ�A2����A2��A2B2��A1B1��x���ڵ�B2���õ��ڶ����ȱ���B1A2B2����B2��B2A3��B1A2��˫�����ڵ�A3����A3��A3B3��A2B2��x���ڵ�B3���õ��������ȱ���B2A3B3���Դ����ƣ��������B6������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��֤���⣬����ʦ�Ѹ�ͬѧ�ǽ�����˼·�����㽫���̺����ɲ���������
��֪��1=��2����A=��E�� ��֤��AD��BE��
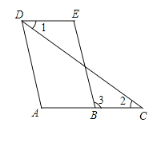
֤�����ߡ�1=��2 ����֪��
��AC��________��___________________________________��
���3= _______ ��___________________________________��
�֡ߡ�A=��E��___________��
���A=______��___________________��
��AD��BE ��_________________________________________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com