【题目】如图的方格地面上，标有编号A、B、C的3个小方格地面是空地，另外6个小方格地面是草坪，除此以外小方格地面完全相同．
（1）一只自由飞行的鸟，将随意地落在图中的方格地面上，问小鸟落在草坪上的概率是多少？
（2）现从3个小方格空地中任意选取2个种植草坪，则刚好选取A和B的2个小方格空地种植草坪的概率是多少（用树形图或列表法求解）？
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案科目：初中数学 来源： 题型：
【题目】阅读理解：已知点P（x0，y0）和直线y=kx+b，则点P到直线y=kx+b的距离，可用公式d=
计算．
例如：求点P（﹣1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（﹣1，2）到直线y=3x+7的距离为：d=
=
=
=
．
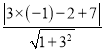根据以上材料，解答下列问题：
（1）求点P（1，﹣1）到直线y=x﹣1的距离；
（2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y=
x+9的位置关系并说明理由；
（3）已知直线y=﹣2x+4与y=﹣2x﹣6平行，求这两条直线之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线y=mx2+nx相交于A（1，3 ），B（4，0）两点．
（1）求出抛物线的解析式；
（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN，求出
的值，并求出此时点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）发现：
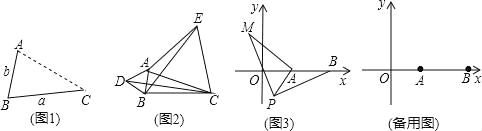
如图1，点A为线段BC外一动点，且BC=a，AB=b．
填空：当点A位于 时，线段AC的长取得最大值，且最大值为 （用含a，b的式子表示）
（2）应用：
点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．
①请找出图中与BE相等的线段，并说明理由；
②直接写出线段BE长的最大值．
（3）拓展：
如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值及此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两家文具店出售同样的钢笔和本子，钢笔每支18元，本子每本2元，甲商店推出的优惠方法为买一支钢笔送两本本子；乙商店的优惠方法为按总价的九折优惠．小丽想购买5支钢笔，本子x本（x≥10）
（1）若到甲商店购买，应付 元（用代数式表示）．
（2）若到乙商店购买，应付 元（用代数式表示）．
（3）若小丽要买的本子为10本，应选择哪家商店？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
