Question

【题目】如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线y=mx2+nx相交于A（1，3 ），B（4，0）两点．

（1）求出抛物线的解析式；

（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；

（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN，求出的值，并求出此时点M的坐标．

Answer 1

【答案】（1）抛物线解析式为y=﹣x2+4x；

（2）存在满足条件的D点，其坐标为（1，0）或（0， ）或（0， ）；理由见解析；

（3）点M的坐标为（+1，2+）．

【解析】解：（1）∵A（1，3），B（4，0）在抛物线y=mx2+nx的图象上，

∴，解得，

∴抛物线解析式为y=﹣x2+4x；（2分）

（2）存在三个点满足题意，理由如下：

当点D在x轴上时，如图1，过点A作AD⊥x轴于点D，

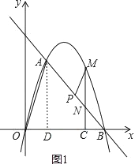
∵A（1，3），∴D坐标为（1，0）；

当点D在y轴上时，设D（0，d），则AD2=1+（3﹣d）2，BD2=42+d2，且AB2=（4﹣1）2+（3）2=36，

∵△ABD是以AB为斜边的直角三角形，

∴AD2+BD2=AB2，即1+（3﹣d）2+42+d2=36，解得d=，

∴D点坐标为（0，）或（0，）；

综上可知存在满足条件的D点，其坐标为（1，0）或（0，）或（0，）；（8分）

（3）如图2，过P作PF⊥CM于点F，

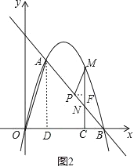
∵PM∥OA，∴Rt△ADO∽Rt△MFP，

∴==3，∴MF=3PF，

在Rt△ABD中，BD=3，AD=3，∴tan∠ABD=，

∴∠ABD=60°，设BC=a，则CN=a，

在Rt△PFN中，∠PNF=∠BNC=30°，∴tan∠PNF==，

∴FN=PF，∴MN=MF+FN=4PF，

∵S△BCN=2S△PMN，∴a2=2××4PF2，

∴a=2PF，∴NC=a=2PF，∴==，

∴MN=NC=×a=a，∴MC=MN+NC=（+）a，

∴M点坐标为（4﹣a，（ +）a），

又M点在抛物线上，代入可得﹣（4﹣a）2+4（4﹣a）=（+）a，

解得a=3﹣或a=0（舍去），OC=4﹣a=+1，MC=2+，

∴点M的坐标为（+1，2+）．（12分）