
【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=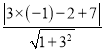 =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
【答案】(1)点P(1,﹣1)到直线y=x﹣1的距离为:d=![]() ;
;
(2)⊙Q与直线y=![]() x+9的位置关系为相切,理由见解析;
x+9的位置关系为相切,理由见解析;
(3)这两条直线之间的距离为2![]()
【解析】解:(1)因为直线y=x﹣1,其中k=1,b=﹣1,
所以点P(1,﹣1)到直线y=x﹣1的距离为:d=![]() =
=![]() =
=![]() =
=![]() ;(3分)
;(3分)
(2)⊙Q与直线y=![]() x+9的位置关系为相切.
x+9的位置关系为相切.
理由如下:圆心Q(0,5)到直线y=![]() x+9的距离为:d=
x+9的距离为:d=![]() =
=![]() =2,
=2,
而⊙O的半径r为2,即d=r,所以⊙Q与直线y=![]() x+9相切;(3分)
x+9相切;(3分)
(3)当x=0时,y=﹣2x+4=4,即点(0,4)在直线y=﹣2x+4,
因为点(0,4)到直线y=﹣2x﹣6的距离为:d=![]() =
=![]() =2
=2![]() ,
,
因为直线y=﹣2x+4与y=﹣2x﹣6平行,所以这两条直线之间的距离为2![]() .(10分)
.(10分)


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒. 
(1)若AB∥x轴,求t的值;
(2)当t=3时,坐标平面内有一点M,使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,且当x=﹣4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的解析式;
(2)当x=﹣ ![]() 时,函数y的值;
时,函数y的值;
(3)当y<1时,自变量x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的方格地面上,标有编号A、B、C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.

(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水星和太阳的平均距离约为5.79×107km,冥王星和太阳的平均距离约是水星和太阳的平均距离的102倍,那么冥王星和太阳的平均距离约为 ( )
A. 5.9×107km B. 5.9×108km C. 5.9×109km D. 5.9×1010km
查看答案和解析>>
科目:初中数学 来源: 题型:
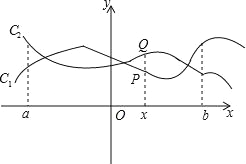
【题目】如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.
(1)判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”,并说明理由;
(2)若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com