
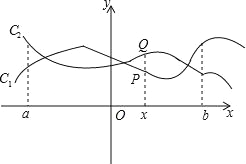
【题目】如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.
(1)判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”,并说明理由;
(2)若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”,求a的取值范围.
【答案】(1)函数y=3x+1与y=2x+2在0≤x≤2上是“相邻函数”,理由见解析;
(2)若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”,则a的取值范围为![]() ≤a≤1.
≤a≤1.
【解析】分析:(1)通过构建函数y=x-1,根据一次函数的性质可得出该函数在0≤x≤2上单调递增,分别代入x=0、x=2即可得出y的取值范围,由此即可得出结论;(2)由函数y=![]() -x与y=xa在0≤x≤2上是“相邻函数”,构造函数y=
-x与y=xa在0≤x≤2上是“相邻函数”,构造函数y=![]() -(a+1)x,根据抛物线的位置不同,令其最大值≤1、最小值≥-1,解关于a的不等式组即可得出结论.
-(a+1)x,根据抛物线的位置不同,令其最大值≤1、最小值≥-1,解关于a的不等式组即可得出结论.
本题解析:(1)函数y=3x+1与y=2x+2在0 ≤ x≤ 2上是“相邻函数”,理由如下:
点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x+2图象上的任一点,
当0≤ x≤ 2时,y1﹣y2=(3x+1)﹣(2x+2)=x﹣1,通过构造函数y=x﹣1并研究它在0≤ x≤ 2上的性质,得到该函数值的范围是﹣1 ≤ y ≤1,所以﹣1 ≤ y1﹣y2 ≤1成立,
因此这两个函数在0 ≤ x ≤2上是“相邻函数”.
(2)∵函数y=x2﹣x与y= x a在0 ≤ x ≤2上是“相邻函数”,
∴构造函数y=x2﹣(a+1)x,在0 ≤ x ≤2上﹣1 ≤ y ≤1.
根据抛物线y=x2﹣(a+1)x对称轴的位置不同,来考虑:
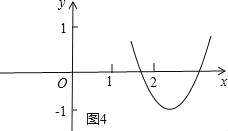
①当![]() ≤0,即a≤﹣1时(图1),
≤0,即a≤﹣1时(图1),
![]() ,解得:a≥
,解得:a≥![]() ,
,
∴此时无解;
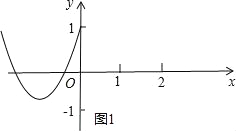
②当0<![]() ≤1,即﹣1<a≤1时(图2),
≤1,即﹣1<a≤1时(图2),
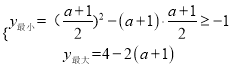 ,解得:
,解得: ![]() ≤a≤1,
≤a≤1,
∴![]() ≤a≤1;
≤a≤1;
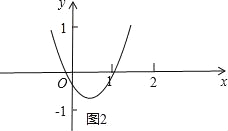
③当1<![]() ≤2,即1<a≤3时(图3),
≤2,即1<a≤3时(图3),
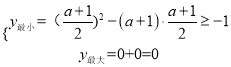 ,解得:﹣3≤a≤1,
,解得:﹣3≤a≤1,
∴此时无解;
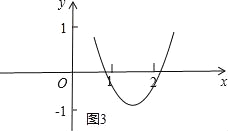
④当2<![]() ,即a>3时(图4),
,即a>3时(图4),
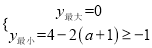 ,解得:a≤
,解得:a≤![]() ,
,
∴此时无解.
综上可知:若函数y=x2﹣x与y=xa在0≤x≤2上是“相邻函数”,则a的取值范围为![]() ≤a≤1.
≤a≤1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=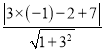 =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.有两边及一角对应相等的两三角形全等
B.若a2=b2 则有a=b
C.方程x2﹣x+1=0有两个不等实根
D.圆的切线垂直于过切点的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
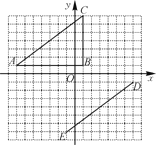
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(-7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,-1),E(-1,-7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°.画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家文具店出售同样的钢笔和本子,钢笔每支18元,本子每本2元,甲商店推出的优惠方法为买一支钢笔送两本本子;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支钢笔,本子x本(x≥10)
(1)若到甲商店购买,应付 元(用代数式表示).
(2)若到乙商店购买,应付 元(用代数式表示).
(3)若小丽要买的本子为10本,应选择哪家商店?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”黄金周期间,为了促销商品,甲、乙两个商店都采取优惠措施,甲店推出八折后再打八折,乙店则一次性六折优惠,若同样价格的商品,下列结论正确的是( )
A. 甲比乙优惠 B. 乙比甲优惠 C. 两店优惠条件相同 D. 不能进行比较
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
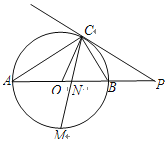
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E. 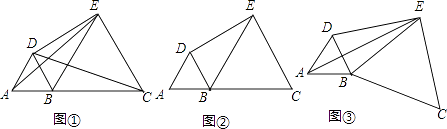
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com