
【题目】如图是一道证明题,李老师已给同学们讲解了思路.请你将过程和理由补充完整.
已知∠1=∠2,∠A=∠E. 求证:AD∥BE.
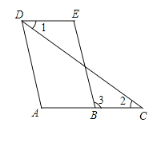
证明:∵∠1=∠2 (已知)
∴AC∥________(___________________________________)
∴∠3= _______ (___________________________________)
又∵∠A=∠E(___________)
∴∠A=______(___________________)
∴AD∥BE (_________________________________________)
【答案】DE 内错角相等,两直线平行 ∠E 两直线平行,内错角相等 已知 ∠3 等量代换 同位角相等,两直线平行
【解析】
根据内错角相等,两直线平行可得AC∥DE,然后根据两直线平行,内错角相等可得∠3=∠E,利用等量代换即可证出∠A=∠3,最后根据同位角相等,两直线平行即可证出结论.
证明:∵∠1=∠2 (已知)
∴AC∥DE(内错角相等,两直线平行)
∴∠3= ∠E(两直线平行,内错角相等)
又∵∠A=∠E(已知)
∴∠A=∠3(等量代换)
∴AD∥BE (同位角相等,两直线平行)
故答案为:DE;内错角相等,两直线平行;∠E;两直线平行,内错角相等;已知;∠3;等量代换;同位角相等,两直线平行.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】数学课堂上,老师提出问题:如图,如何在该图形中数出黑色正方形的个数,以下是两位同学的做法:
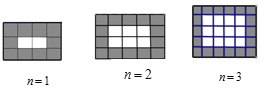
(1)甲同学的做法为:
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
……则在第![]() 个图形中,黑色正方形的个数共有 (无需化简)
个图形中,黑色正方形的个数共有 (无需化简)
(2)乙同学的做法为:
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
……则在第![]() 个图形中,黑色正方形的个数共有 (无需化简)
个图形中,黑色正方形的个数共有 (无需化简)
(3)数学老师及时肯定了两位同学的做法,从而可以得到等式
(4)请利用学习过的知识验证(3)问中的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置。

查看答案和解析>>
科目:初中数学 来源: 题型:
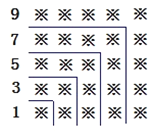
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的值;
的值;
(2)探究:当点![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根据(2)中的结论,请构造图形求代数式![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
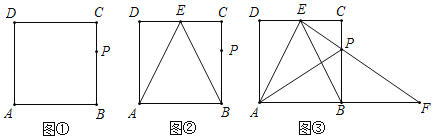
【题目】如图,在矩形ABCD中,AB═2,AD=![]() ,P是BC边上的一点,且BP=2CP.
,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条体下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com